1. 결정트리(decision tree) 알고리즘
1-1. 결정트리란?
- 결정트리는 데이터의 특성(Feature)에 따라 데이터 집합을 분할해 나가면서 예측 모델을 구축하는 알고리즘입니다.
- 트리 구조를 사용하여 결정 규칙을 표현하며, 각 노드는 특성의 조건에 따라 데이터를 분할하는 결정을 나타냅니다.
1-2. CART 알고리즘
- CART(Classification And Regression Trees)는 분류와 회귀 모두에 사용될 수 있는 결정트리 구축 방법론입니다.
- 트리를 구성할 때, 데이터를 가장 잘 분할할 수 있는 특성과 그 값을 찾아내는 과정을 반복합니다.
- 분할 기준으로는 주로 지니 계수(Gini Index) 또는 정보 이득(Information Gain)을 사용합니다.
1-3. 노드 분할 기준
- 범주형 특징 분할
- 범주형 특징은 해당 범주에 속하는 데이터를 기준으로 노드를 분할합니다.
- 예를 들어, ‘색상’이라는 특징에 대해 ‘빨강’, ‘파랑’, ‘초록’과 같은 범주가 있다면, 이 범주에 따라 데이터를 분할합니다.
- 수치형 특징 분할
- 수치형 특징은 특정 수치를 기준으로 데이터를 분할합니다.
- 예를 들어, ‘키’라는 특징에 대해 특정 값(예: 160cm)을 기준으로 더 큰 값과 작은 값으로 데이터를 분할합니다.
1-4. 균일도 측정 방법
- 지니 계수(Gini Index)
- 지니 계수는 데이터 집합의 불순도를 측정하는 방법으로, 0에 가까울수록 데이터 집합의 순도가 높다는 것을 의미합니다.
- 계산 방식은 1에서 모든 클래스의 데이터 비율의 제곱을 뺀 값으로, 값이 낮을수록 균일도가 높은 것으로 평가됩니다.
- 균일도가 높은 데이터 세트를 우선적으로 분할하는 것이 결정트리의 기본 원칙입니다.
2. 결정트리 만들기
2-1. 결정트리 만들고 결정경계 확인하기
Python
from sklearn.tree import DecisionTreeClassifier # 하나의 의사결정트리
tree_model = DecisionTreeClassifier()
tree_model.fit(X_train_std, y_train)
tree_model.predict(X_test_std)
# array([0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 2, 0, 0, 2, 2, 0, 1, 1, 0, 1, 1,
1, 1, 2, 1, 2, 2, 1, 1])- tree_model.score(X_test_std, y_test) = 0.9666666666666667
Python
plot_decision_regions(X=X_train_std,
y=y_train,
classifier=tree_model)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('images/03_05.png', dpi=300)
plt.show()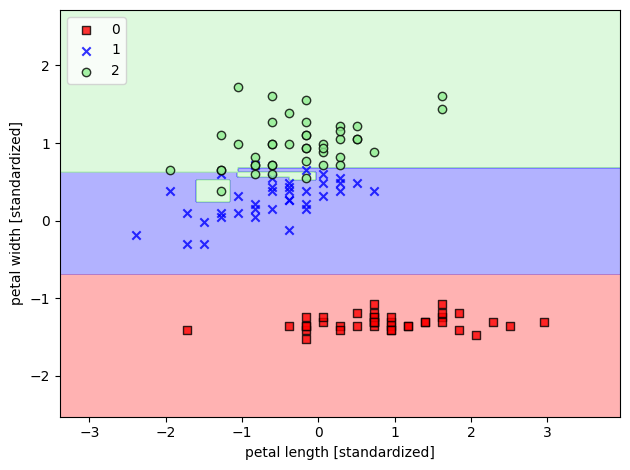
2-2. 결정트리 확인하기
Python
from sklearn import tree
tree.plot_tree(tree_model) # fit() 메서드를 통해서 X_train_std을 학습한 결과를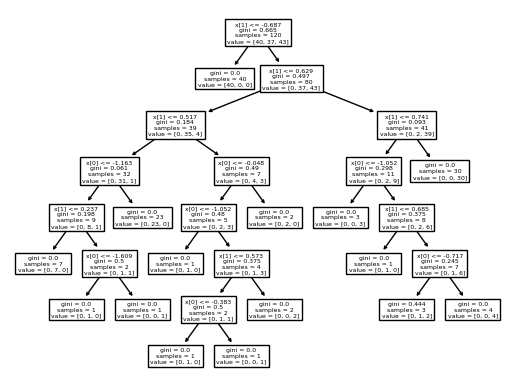
2-3. max_dept 주기
Python
from sklearn.tree import DecisionTreeClassifier # 하나의 의사결정트리
tree_model = DecisionTreeClassifier(max_depth=4, random_state=42)
tree_model.fit(X_train_std, y_train)
tree_model.predict(X_test_std)
from sklearn import tree
tree.plot_tree(tree_model) # fit() 메서드를 통해서 X_train_std을 학습한 결과를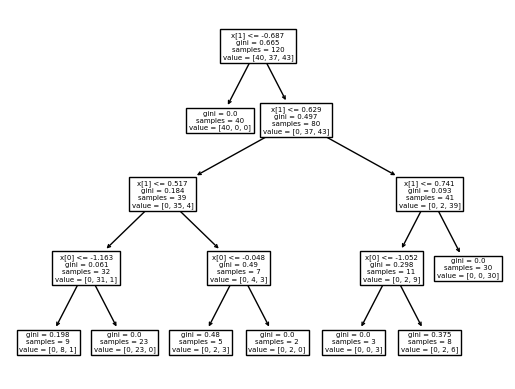
2-4. feature_importances_
Python
tree_model.feature_importances_ #array([0.02010426, 0.97989574])feature_importances_속성은 결정트리 기반의 모델(예를 들어, 결정트리, 랜덤 포레스트, 그래디언트 부스팅)에서 각 특성(feature)이 예측 결과에 미치는 상대적 중요도를 나타내는 지표입니다. 이 값은 0과 1 사이의 값을 가지며, 모든 특성의 중요도 합은 1이 됩니다. 특성의 중요도는 해당 특성을 사용한 분할에서 불순도 감소량(예: 지니 불순도, 엔트로피 감소량)을 기반으로 계산됩니다.- 예제에서 제시된
feature_importances_배열은 두 개의 특성[0.02010426, 0.97989574]에 대한 중요도를 나타냅니다. 이는 첫 번째 특성(x[0])이 약 2%의 중요도를 가지고 있으며, 두 번째 특성(x[1])이 약 98%의 중요도를 가진다는 것을 의미합니다. 즉,x[1]특성이 모델을 만드는 데 있어 훨씬 더 큰 영향을 미치고 있음을 나타냅니다.
2-5. min samples split 걸기
Python
from sklearn.tree import DecisionTreeClassifier # 하나의 의사결정트리
tree_model = DecisionTreeClassifier(random_state=42, min_samples_split=40)
tree_model.fit(X_train_std, y_train)
tree_model.score(X_test_std, y_test) # 0.9- `min_samples_split`: 노드를 분할하기 위한 최소 샘플 수입니다. 이 값을 조절함으로써 모델의 과적합을 방지할 수 있습니다.
Python
from sklearn import tree
tree.plot_tree(tree_model) # fit() 메서드를 통해서 X_train_std을 학습한 결과를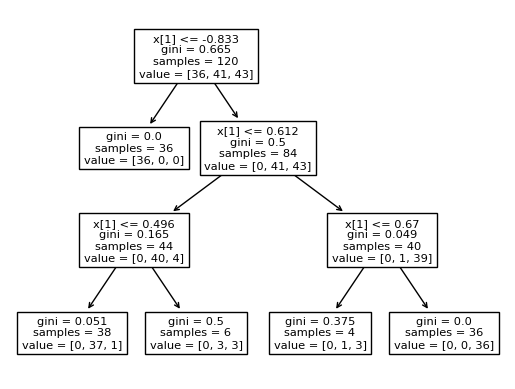
2-6. 결정트리의 장점
- 이해하기 쉬운 알고리즘
- 직관적인 결정 규칙: 결정트리는 “if-else” 규칙의 연속으로 데이터를 분류하거나 회귀 분석을 수행합니다. 이러한 규칙은 사람이 이해하기 쉽습니다.
- 시각화 용이성: 트리 구조를 그래프로 쉽게 시각화할 수 있으며, 이는 모델의 결정 과정을 이해하는 데 도움을 줍니다.
- 결정 과정의 투명성: 각 결정 노드에서의 분할 기준과 경로를 통해 최종 결정에 이르는 과정을 명확하게 파악할 수 있습니다.
- 비선형 결정경계
- 비선형 데이터 처리 능력: 결정트리는 선형 모델로 해결하기 어려운 비선형 패턴도 잘 포착할 수 있습니다.
- 복잡한 결정 경계 형성: 여러 조건의 결합으로 복잡한 결정 경계를 형성할 수 있어 다양한 데이터셋에 적용 가능합니다.
3. 불순도
3-1. 지니 불순도(Gini Impurity)
- 정의: 노드 내에서 임의로 선택한 레이블이 잘못 분류될 확률을 측정합니다. 지니 불순도는 0(완전 순수)에서 0.5(완전 불순) 사이의 값을 가집니다.
- 계산 공식: p⋅(1−p)+(1−p)⋅(1−(1−p))
- 특징: 지니 불순도는 계산이 간단하며, 작은 값일수록 노드의 순수도가 높다는 것을 의미합니다.
3-2. 엔트로피(Entropy)
- 정의: 노드의 불확실성(혼란도)을 측정합니다. 엔트로피가 높을수록 불순도가 높아, 정보 이득(Information Gain)이 큰 분할을 찾는 데 유용합니다.
- 계산 공식: −p⋅log2(p)−(1−p)⋅log2(1−p)
- 특징: 엔트로피는 지니 불순도보다 노드의 불확실성을 민감하게 반영합니다. 따라서, 더 복잡한 모델을 만들 가능성이 있습니다.
3-3. 분류 오류(Misclassification Error)
- 정의: 노드에서 가장 빈번한 클래스를 예측값으로 사용할 때, 잘못 분류될 확률을 측정합니다.
- 계산 공식: =1−max(p,1−p)
- 특징: 분류 오류는 가장 단순한 불순도 측정 방법으로, 주로 학습 과정이 아닌 가지치기 단계에서 사용됩니다.
3-4. 시각화 및 비교
Python
import matplotlib.pyplot as plt
import numpy as np
def gini(p):
return p * (1 - p) + (1 - p) * (1 - (1 - p))
def entropy(p):
return - p * np.log2(p) - (1 - p) * np.log2((1 - p))
def error(p):
return 1 - np.max([p, 1 - p])
x = np.arange(0.0, 1.0, 0.01)
ent = [entropy(p) if p != 0 else None for p in x]
sc_ent = [e * 0.5 if e else None for e in ent]
err = [error(i) for i in x]
fig = plt.figure()
ax = plt.subplot(111)
for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err],
['Entropy', 'Entropy (scaled)',
'Gini impurity', 'Misclassification error'],
['-', '-', '--', '-.'],
['black', 'lightgray', 'red', 'green', 'cyan']):
line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)
ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
ncol=5, fancybox=True, shadow=False)
ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
plt.ylim([0, 1.1])
plt.xlabel('p(i=1)')
plt.ylabel('impurity index')
# plt.savefig('images/03_19.png', dpi=300, bbox_inches='tight')
plt.show()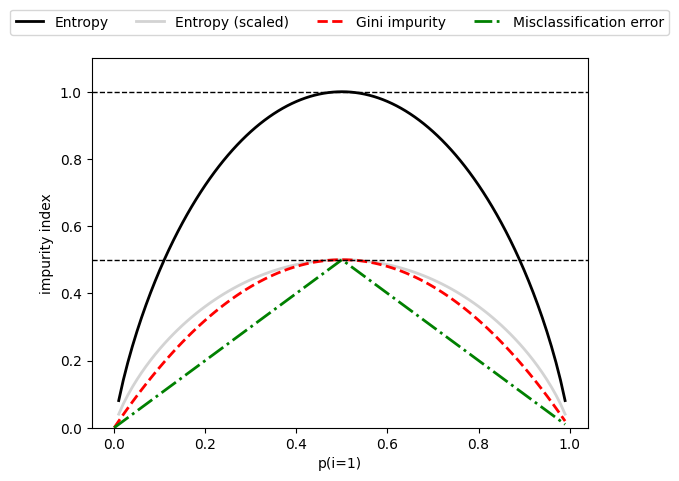
4. 랜덤 포레스트로 여러개의 결정 트리 연결
4-1. 여러 개의 결정 트리를 결합한 이유
- 오버피팅 감소: 단일 트리는 훈련 데이터에 과적합되기 쉬운 반면, 여러 트리의 결과를 평균내어 오버피팅을 줄일 수 있습니다.
- 정확도 향상: 여러 개의 결정 트리가 독립적으로 예측을 수행하고, 그 결과를 집계함으로써 더 정확한 예측이 가능합니다.
- 특성 선택의 다양화: 각 트리는 무작위로 선택된 특성의 부분 집합을 사용하여 학습하므로, 다양한 특성 조합이 모델에 반영됩니다.
4-2. 일반화된 모델의 중요성
- 새로운 데이터에 대한 성능: 일반화된 모델은 본 적 없는 새로운 데이터에 대해서도 잘 예측해야 합니다. 이는 모델의 실질적인 성능을 나타냅니다.
- 모델의 견고성: 랜덤 포레스트는 다양한 데이터 변동성에 대해 견고한 모델을 생성할 수 있으며, 이는 실제 환경에서의 사용에 있어 중요한 요소입니다.
Python
# 여러개의 트리가 만든 의사결정나무의 평균값을 가지고 클래스를 분류하는 분류모델
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=50, n_jobs=-1) # n_jobs = -1 cpu의 가용자원을 모두 사용해라
forest.fit(X_train, y_train)
forest.score(X_test, y_test) # 0.9666666666666667
forest.feature_importances_ # array([0.21448133, 0.78551867])
forest.predict_proba(X_test)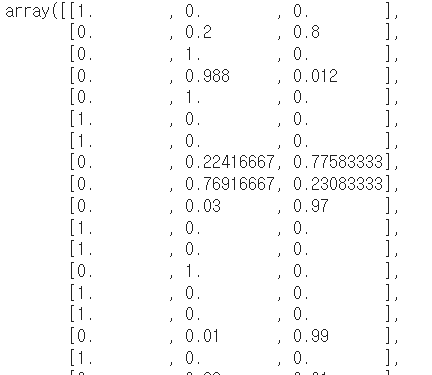
4-3. 결정경계 확인
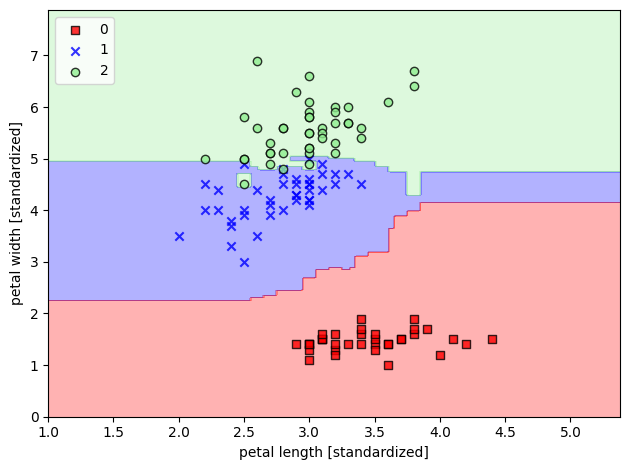
5. K Nearest Neighbors (k-최근접 이웃 분류 알고리즘)
5-1. KNN의 기본 원리
- 가까운 이웃 찾기: 주어진 새로운 데이터 포인트에 대해, 가장 가까운 K개의 이웃을 찾아 이들의 정보를 사용하여 분류합니다.
- 거리 측정 방식: 이웃을 찾을 때는 주로 유클리드 거리, 맨해튼 거리 등의 거리 측정 방식을 사용합니다.
- 투표 기반 분류: 가장 많이 나타나는 클래스를 새로운 데이터 포인트의 클래스로 예측합니다.
5-2. KNN 구현 방법
- 데이터 준비: sklearn의
make_classification함수를 사용하여 분류를 위한 더미 데이터를 생성합니다. - 모델 생성과 학습:
KNeighborsClassifier를 사용하여 KNN 모델을 생성하고,fit메소드로 데이터에 적합시킵니다. - 예측과 시각화:
predict메소드를 사용하여 새로운 데이터 포인트의 클래스를 예측하고, 결과를 시각화합니다.
5-3. KNN의 특징과 활용
- 게으른 학습(Lazy Learner): 훈련 데이터로부터 명시적인 학습 모델을 생성하지 않고, 예측 시점에 거리 계산을 통해 분류를 수행합니다.
- 매개변수 K의 중요성: K값의 선택은 모델의 성능에 큰 영향을 미칩니다. 너무 작으면 노이즈에 민감해지고, 너무 크면 경계가 불분명해질 수 있습니다.
- 스케일링의 중요성: 변수의 스케일이 다르면 거리 계산에 영향을 미쳐 성능이 저하될 수 있습니다. 따라서, 특성 스케일링(preprocessing)이 필요합니다.
Python
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_classification
fig, axes = plt.subplots(3, 3)
fig.set_size_inches(10, 10)
for i in range(9):
# 더미 데이터 생성
X, y = make_classification(n_samples=50, n_features=2, n_informative=2, n_redundant=0, random_state=30)
blue = X[y==0]
red = X[y==1]
# 랜덤한 새로운 점 생성
newcomer = np.random.randn(1, 2)
# K
K = 3*(i//3+1)
axes[i//3, i%3].scatter(red[:,0], red[:, 1], 80, 'r', '^')
axes[i//3, i%3].scatter(blue[:,0], blue[:, 1], 80, 'b', '^')
axes[i//3, i%3].scatter(newcomer[:, 0], newcomer[:, 1], 80, 'g', 'o')
# n_neighbors=3
knn = KNeighborsClassifier(n_neighbors=3*(i//3+1))
print(3*(i//3+1))
knn.fit(X, y)
pred = knn.predict(newcomer)
# 표기
axes[i//3, i%3].annotate('red' if pred==1 else 'blue', xy=newcomer[0], xytext=(newcomer[0]), fontsize=12)
plt.tight_layout()
plt.show()
- KNN 모델 생성 및 학습:
KNeighborsClassifier클래스를 사용하여 KNN 모델을 생성하고, 생성된 더미 데이터셋에 대해 학습(fit메소드 사용)을 진행합니다. 여기서n_neighbors매개변수에는 각 이웃의 개수K를 지정합니다. 이 예시에서는K를 3부터 시작하여 3의 배수로 증가시키면서 다양한K값에 대한 모델의 성능을 시각화합니다. - 결과 시각화: 9개의 서브플롯을 생성하여 다양한
K값에 대한 KNN 분류 결과를 시각화합니다. 각 서브플롯은K값의 변화에 따른 분류 결과의 변화를 보여주며, 이를 통해K값이 결과에 미치는 영향을 관찰할 수 있습니다.
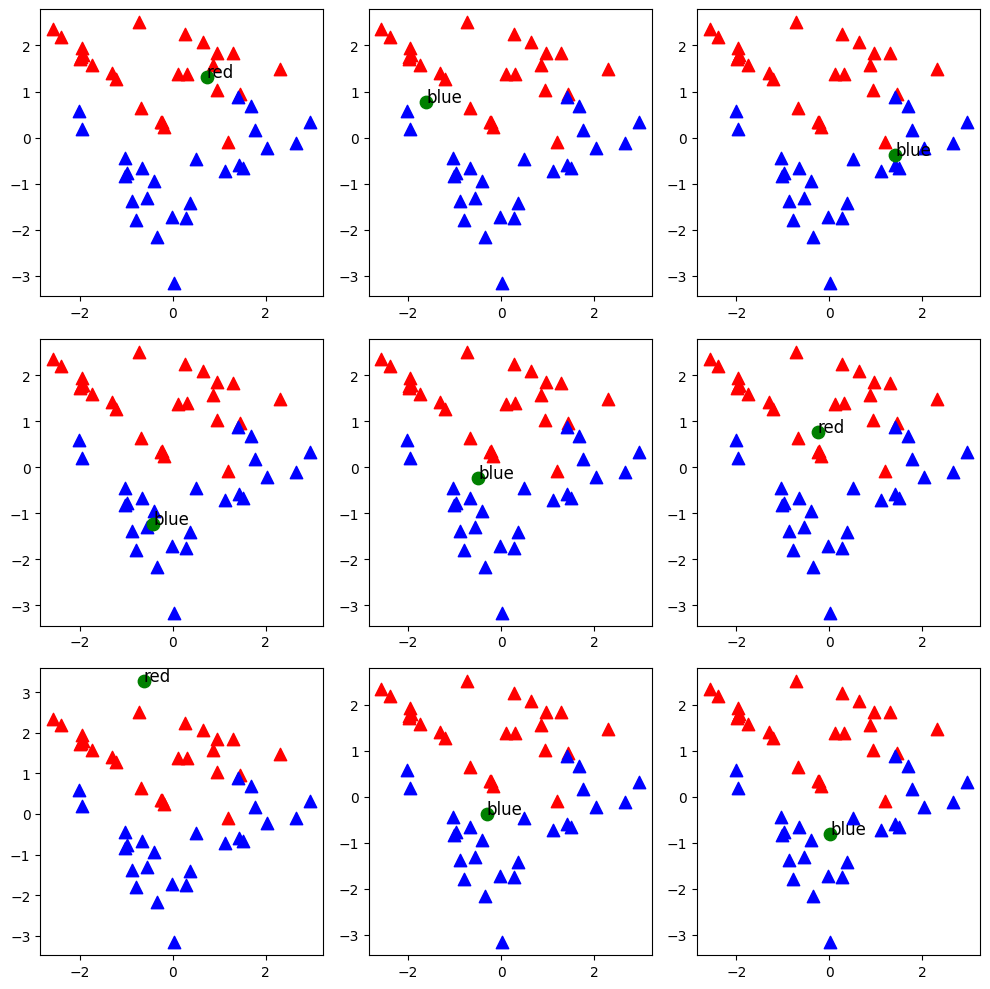
KNN의 주요 파라미터
n_neighbors: 이웃의 수(K)를 의미하며, 이 값에 따라 모델의 복잡도가 결정됩니다. K가 너무 작으면 모델은 노이즈에 민감해지고, 너무 크면 분류 경계가 과도하게 단순화됩니다.metric: 데이터 포인트 간의 거리를 측정하는 방법을 지정합니다. 일반적으로 유클리드 거리(Euclidean distance)가 사용되지만, 맨해튼 거리(Manhattan distance)나 민코프스키 거리(Minkowski distance) 등 다양한 거리 측정 방법이 사용될 수 있습니다.
모수 모델(Parametric Models)
모수 모델은 고정된 수의 파라미터를 사용하여 데이터로부터 모델을 학습합니다. 이러한 모델은 학습 과정에서 최적의 파라미터(가중치와 편향)를 찾아내며, 이 파라미터들은 모델이 데이터를 얼마나 잘 예측하는지를 결정합니다. 모수 모델의 핵심 가정은 데이터의 분포를 고정된 수의 파라미터로 충분히 표현할 수 있다는 것입니다.
모수 모델(모델 기반 학습)핵심 개념
- 파라미터 학습: 모델 기반 접근 방식에서는 가중치(weights)와 편향(bias) 같은 모델 파라미터를 학습 데이터를 통해 최적화합니다. 이 과정은 주로 손실 함수(loss function)를 최소화하는 파라미터를 찾는 것을 목표로 합니다.
- 일반화: 학습된 모델은 보지 못한 새로운 데이터에 대해 일반화될 수 있어야 합니다. 즉, 훈련 데이터에만 잘 작동하는 것이 아니라, 새로운 데이터에 대해서도 잘 예측할 수 있어야 합니다.
종류
- 퍼셉트론: 가장 간단한 형태의 신경망으로, 입력 특성의 선형 조합을 통해 예측을 수행합니다. 퍼셉트론은 입력 데이터에 대한 가중치와 하나의 편향 파라미터를 학습합니다.
- 로지스틱 회귀: 선형 결합을 사용하지만, 결과를 0과 1 사이의 확률로 변환하는 로지스틱 함수(시그모이드 함수)를 적용합니다. 이 모델 또한 데이터와 레이블 간의 관계를 설명하는 데 사용되는 고정된 수의 파라미터(가중치와 편향)를 학습합니다.
- SVM(선형): 선형 서포트 벡터 머신은 데이터를 분류하기 위해 결정 경계(하이퍼플레인)를 찾는 모델입니다. 이 결정 경계는 학습 데이터에 대해 마진을 최대화하는 방식으로 결정됩니다. 선형 SVM은 고정된 수의 파라미터(가중치와 편향)를 사용합니다.
비모수 모델(Non-parametric Models)
비모수 모델은 고정된 수의 파라미터를 가지지 않습니다. 대신, 모델의 복잡성은 주어진 데이터의 양에 따라 증가할 수 있습니다. 이러한 모델은 데이터의 구조나 패턴을 학습하는 데 더 많은 유연성을 제공하지만, 과적합(overfitting)의 위험이 더 높을 수 있습니다.
비모수 모델(인스턴스 기반 학습) 핵심개념
- 유사성 측정: 새로운 데이터 포인트에 대한 예측을 수행할 때, 저장된 훈련 데이터 인스턴스들과의 유사성을 측정합니다. 이 유사성은 보통 거리 측정(metric)을 통해 계산됩니다.
- 메모리 기반: 이 접근 방식은 학습 데이터를 모두 메모리에 보관합니다. 따라서, 새로운 예측을 할 때마다 저장된 데이터와의 비교를 통해 예측을 수행합니다.
종류
- SVM(커널형): 선형 SVM을 확장하여 비선형 데이터도 처리할 수 있도록 하는 커널 트릭을 사용합니다. 커널 함수를 통해 입력 데이터를 고차원 공간으로 매핑함으로써, 비선형 관계를 모델링할 수 있습니다. 커널 함수의 선택과 파라미터는 데이터의 양과 구조에 따라 달라질 수 있으며, 이로 인해 모델의 파라미터 수가 사실상 무한대로 증가할 수 있습니다.
- KNN(K-Nearest Neighbors): KNN은 주어진 데이터 포인트의 가장 가까운 K개의 이웃을 찾아 그 이웃들의 레이블을 기반으로 분류하거나 회귀를 수행합니다. KNN은 모든 훈련 데이터를 모델의 “파라미터”로 사용하기 때문에, 데이터가 늘어남에 따라 필요한 파라미터의 수도 증가합니다.
- 결정 트리 / 랜덤 포레스트: 이 모델들은 훈련 데이터를 기반으로 결정 규칙을 학습하며, 트리의 깊이나 노드의 수는 데이터의 양과 복잡성에 따라 달라집니다. 랜덤 포레스트는 여러 개의 결정 트리를 조합하여 사용하기 때문에, 모델의 복잡성은 더욱 증가할 수 있습니다.