교차 검증은 모델의 일반화 능력을 평가하는 기법으로, 데이터를 여러 부분으로 나누어 일부는 훈련에, 나머지는 검증에 사용하는 방식입니다. 이를 통해 모델이 새로운 데이터에 대해 얼마나 잘 작동하는지를 평가할 수 있습니다. 교차 검증의 한 방법으로 널리 사용되는 GridSearchCV는 다양한 하이퍼파라미터의 조합을 시험하여 최적의 조합을 찾아내는 방법입니다.
하이퍼파라미터 튜닝은 모델의 성능을 최대화하기 위해 모델의 설정 값을 조정하는 과정입니다. 이 과정에서 GridSearchCV와 같은 도구를 사용하여 다양한 설정의 조합을 자동으로 실험하고, 가장 좋은 결과를 내는 조합을 선택합니다. 이렇게 선택된 하이퍼파라미터는 모델의 예측 성능을 크게 향상시킬 수 있습니다.
높은 예측 정확도를 달성하기 위해서는 체계적이고 다양한 평가 지표를 활용해야 합니다. 이 과정에서 사용되는 주요 평가 지표로는 오차 행렬(Confusion Matrix), 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), F1 점수(F1-score), 그리고 ROC-AUC 등이 있습니다. 각 지표는 모델의 다른 측면을 평가하여, 모델의 강점과 약점을 종합적으로 이해하는 데 도움을 줍니다.
1. 교차 검증과 최적 하이퍼파라미터 튜닝
1-1. GridSearchCV – 교차 검증
- GridSearchCV – 교차 검증
- 다양한 모델의 훈련 과정을 자동화하고, 교차 검사를 사용해 최적 값을 제공하는 도구
- 하이퍼파라미터를 순차적으로 적용하면서 편리하게 최적의 파라미터 도출
- 격자형식으로 dict 구조의 하이퍼파라미터값 적용
# 클래스 임포트 (모델, 모델을 나 대신 돌려줄 더 큰 객체)
from sklearn.model_selection import GridSearchCV
parameter= {"max_depth": [1,2,3,4,5], "min_samples_split":range(2, 5)}
# 클래스를 통한 인스턴스 생성 - 우리가 측정하고 싶은 평가 기준, 넣어보고 싶은 파라미터덩어리를 넘겨주면서
grid_dtree = GridSearchCV(dt_clf, param_grid=parameter)
# 더 큰 객체한테 모델과 결과를 확인하도록 요청
grid_dtree.fit(X_train, y_train)
- param_grid : param_grid 라는 파라미터에 우리가 도하려는 모델에 대한 파라미터를 dict 형태로 넘겨줍니다
- 이 모델은 param_grid 에 들어간 형태로 max_Depth를 행으로 min_sample_split을 열로 해서 위와 같은 파라미터를 설정시 amx_Depth 5 * minsamples_split 3 = 15번을 수행하게 된다. 또 CV 가 5가 기본값이여서 15 * 5 의 75번을 학습한다.
- grid_dtree = GridSearchCV(dt_clf,cv=7, param_grid=parameter) : cv 값 조정 방법
1-2. 파라미터 값 확인
- grid_dtree.best_estimator_ # DecisionTreeClassifier(max_depth=3)
- grid_dtree.best_params_ # {‘max_depth’: 3, ‘min_samples_split’: 2}
- grid_dtree.best_score_ # 0.975
- pd.DataFrame(grid_dtree.cv_results_) # mean_fit_time 학습의 평균 시간, mean_score_time : 평가 평균 시간, rank_test_score : 학습 점수와 같은 모델의 전반적인 내용을 알려줌
1-3. 그리드 서치 장점
- 여러개의 파라미터를 일일히 손으로 수정하면서 결과를 확인하지 않아도 된다.
- n 번의 교차검증을 수행한다. -> score는 5(CV의 기본값)번의 평균이기 떄문에 신뢰도도 올라갑니다.
- 우리가 train 데이터를 가져가 쓰면 알아서 test 데이터로 사용하면서 겹치지 않게 결과를 보여주고 잇따.
1-4. RandomizedSearchCV
# 모델 차원의(알고리즘) 알고리즘을 정교화하기 위한 최적의 파라미터를 찾는 법을 공부하는 중
# RandomizedSearchCV - 최적의 파라미터를 찾기 위한 범위를 정해주고 최대 시도의 횟수를 정해주면 그 안에서 최적의 조합을 바꿔가며 찾아준다.
from sklearn.model_selection import RandomizedSearchCV
from sklearn.tree import DecisionTreeClassifier
parameter = {'max_depth' : range(1,5), 'min_samples_split':range(2,5)}
dt_clf = DecisionTreeClassifier()
random_dtree = RandomizedSearchCV(dt_clf, param_distributions=parameter, n_iter=10 )
random_dtree.fit(X_train, y_train)- # param_distributions 파라미터의 분포로 넘겨준다.
- # n_iter=10 10번만 최적의 방향을 찾는 방식으로 시도해줘
1-5. 파라미터 값 확인
- random_dtree.best_estimator_ : DecisionTreeClassifier(max_depth=3, min_samples_split=4)
- random_dtree.best_score_ : 0.975
1-6. GridSearchCV VS RandomizedSearchCV
프로젝트의 요구 사항과 리소스에 따라 달라집니다. 빠른 시간 내에 괜찮은 결과를 원한다면 RandomizedSearchCV, 최적의 결과를 원한다면 GridSearchCV를 선택할 수 있습니다.
2. 좋은 데이터를 찾기 위한 과정
- 지금까지 작업은 모델에 넣을 수 잇는 최적의 파라미터를 찾아서 정확도를 올리고 교차 검증(cv : cross validate)을 통해서 신뢰성을 확인하였다.
- 그러면 학습에 사용되는 데이터가 어떤 데이터가 좋은지 SequatialFeatureSelector를 통해 몇 개의 특성으로 데이터를 분석하면 좋을지를 알아보자
2-1. SequentialFeatureSelector 이란
- 순차적 특성 선택(Sequential Feature Selector)은 머신러닝 모델의 성능을 향상시키기 위해, 데이터셋 내의 특성(또는 변수) 중 가장 유의미한 부분집합을 선택하는 방법입니다.
- 이 과정은 특히 특성의 수가 많아질 때 중요하게 되는데, 이는 모든 가능한 특성의 조합을 평가하기에는 계산 비용이 너무 많이 들기 때문입니다.
2-2. SequentialFeatureSelector 사용
from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier(max_depth=3)
sfs = SequentialFeatureSelector(dt_clf) # n_features_to_select
sfs.fit(X_train, y_train)
sfs.get_support() # array([False, False, True, True])get_support메소드는 2번째와 3번째 특성이 유의미하다고 판단했음을 보여줍니다.
sfs = SequentialFeatureSelector(dt_clf, n_features_to_select = 3)
#result : array([ True, False, True, True])n_features_to_select를 3으로 설정함으로써, 알고리즘이 유의미한 3개의 특성을 선택하게 됩니다. 이는 기존에 버릴 예정이었던 특성 중에서도 가치가 있는 것을 포함시킵니다.
X_train_sfs = sfs.transform(X_train)
''' result : array([[6.7, 4.7, 1.5],
[7.7, 6.9, 2.3],
[5.2, 1.4, 0.2],
[5. , 1.6, 0.6], .... '''transform메소드를 사용하여 선택된 특성만을 포함하는 새로운 훈련 데이터 세트를 생성합니다.
2-3. 시각화
from sklearn.feature_selection import SequentialFeatureSelector
import matplotlib.pyplot as plt
dt_clf = DecisionTreeClassifier(max_depth=3)
scores = []
for n_features in range(1, 4):
sfs = SequentialFeatureSelector(dt_clf, n_features_to_select=n_features, n_jobs=-1)
sfs.fit(X_train, y_train)
print(f'{n_features}일 때: {sfs.support_}')
f_mask = sfs.support_
dt_clf.fit(X_train[:, f_mask], y_train)
scores.append(dt_clf.score(X_train[:, f_mask], y_train))
plt.plot(range(1, 4), scores, marker='o')
plt.ylim([0.7, 1.02])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.tight_layout()
plt.show()- result :
- 1일 때: [False False False True]
- 2일 때: [False False True True]
- 3일 때: [ True False True True]
- 해석 :
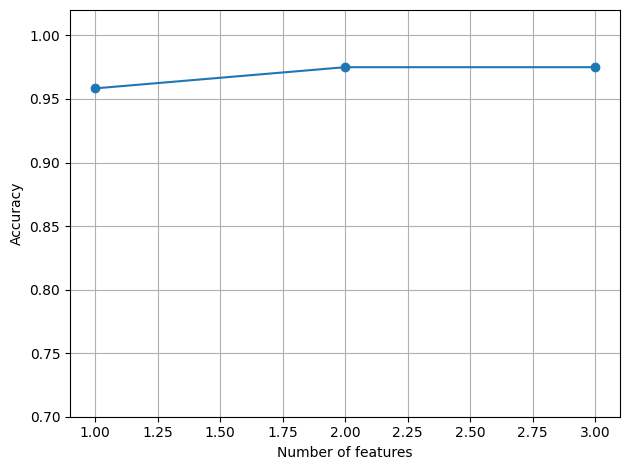
- 위의 그래프는 결정 트리 분류기의 특성 선택에 대한 정확도를 나타내고 있습니다. 특성의 수가 증가함에 따라 모델의 정확도가 어떻게 변하는지 보여줍니다.
- 결과를 보면, 특성이 하나일 때 정확도가 가장 낮습니다. 이는 단일 특성만 사용하여 모델을 학습했을 때 모델이 학습 데이터를 잘 설명하지 못함을 의미할 수 있습니다. 특성이 하나일 때 사용된 특성은 네 번째 특성입니다(
[False False False True]). - 특성이 두 개일 때, 정확도가 증가하여 모델이 더 나은 성능을 보입니다. 이때 사용된 특성은 세 번째와 네 번째 특성입니다(
[False False True True]). - 마지막으로, 특성이 세 개일 때 정확도는 약간 감소하거나 동일한 수준으로 유지되었습니다. 이 경우 모든 특성을 제외하고 첫 번째, 세 번째, 네 번째 특성이 사용되었습니다(
[True False True True]). - 정확도가 가장 높은 것은 특성이 두 개 또는 세 개 일 때입니다. 특성이 두 개일 때와 세 개일 때의 차이가 없습니다. 따라서 모델의 복잡성과 계산 비용을 절감하기 위해 특성 두 개를 사용하는 것이 좋습니다.
2-4. 접근
- 실제로는 좋은 데이터를 고른 뒤 좋은 알고리즘을 선택하는 단계로 진행한다.
3. 모델 성능 평가 지표
모델 성능 평가:
- 실제값과 예측값의 오차를 통해 모델의 정확도를 측정한다.
- 오차가 없다는 것(실제값 – 예측값 = 0)은 모델이 완벽하게 예측했다는 의미이지만, 현실에서는 거의 불가능하다.
- 오차의 허용 범위를 설정하여 모델의 성능을 결정한다.
모델 평가의 목적:
- 최적의 모델을 선택하고 과적합을 방지하기 위해 모델의 일반화 능력을 평가한다.
- 지도 학습에서만 적용 가능하며, 정답이 있는 데이터를 통해 모델의 예측 성능을 검증한다.
모델 평가 지표:
- 회귀 분석의 경우: MSE, RMSE, MAE 등의 지표를 활용하여 수치적 오차를 측정한다.
- 분류 문제의 경우: 정확도, 정밀도, 재현율, F1 점수 등을 통해 모델의 분류 성능을 평가한다.
Training과 Validation 성능 비교:
- Training과 Validation 세트에서의 성능이 유사할수록 일반화된 모델이라고 판단한다.
- Training 성능은 우수하지만 Validation 성능이 저하될 경우, 과적합의 신호로 해석한다.
- 교차 검증(Cross-validation)을 통해 모델의 안정성을 확인한다.
과적합(Overfitting) 진단 및 해결:
- 과적합을 진단하기 위해 학습 곡선을 분석하고, Training과 Validation의 성능 차이를 관찰한다.
- 정규화 기법(L1, L2 규제), 데이터 증강, 조기 종료(Early Stopping) 등을 통해 과적합을 방지한다.
- 특성 선택 및 차원 축소를 통해 모델의 복잡성을 줄인다.
모델 선택 및 최적화:
- 여러 모델을 비교하고 하이퍼파라미터 튜닝을 통해 최적의 모델을 선택한다.
- 그리드 검색(Grid Search), 랜덤 검색(Random Search), 베이지안 최적화 등의 방법을 사용한다.
- 모델의 해석 가능성과 복잡성 사이의 균형을 고려하여 선택한다.
| 모델링 목적 | 목표 변수 유형 | 모델 예시 | 평가 방법 |
|---|---|---|---|
| Classification(분류) | 범주형 | 로지스틱회귀, 의사결정나무, SVM | 정확도, 정밀도, 재현율, F1-score 등 |
| Prediction(예측/회귀) | 연속형 | 선형회귀 | MSE, RMSE, MAE, MAPE 등 |
4. 분류모델 성능 평가
- 1) 오차 행렬(Confusion Matrix)
- 2) 정확도(Accuarcy)
- 3) 정밀도(Precision)
- 4) 재현율(Recall)
- 5) F1-score
- 6) ROC – AUC
4-1. 오차 행렬(Confusion Matrix)
- 오차 행렬(Confusion Matrix)의 정의
- 분류 모델의 성능을 평가하기 위한 행렬로, 실제 클래스와 예측 클래스를 교차하여 배열한 표
- 모델이 어떻게 예측을 잘못하고 있는지를 직관적으로 파악할 수 있는 도구
- 이진 분류에서의 오차 행렬
- 이진 분류는 결과가 ‘Positive’ 또는 ‘Negative’ 두 가지 중 하나로 분류되는 경우를 말함
- 오차 행렬은 True Positive, False Positive, True Negative, False Negative 네 가지 요소로 구성됨
- 오차 행렬의 구성 요소
- True Negative (TN)
- 실제 값이 ‘Negative’이며, 모델도 ‘Negative’로 정확히 예측한 경우의 수
- False Positive (FP) – 제1종 오류
- 실제 값은 ‘Negative’이지만, 모델이 오류를 범하여 ‘Positive’로 잘못 예측한 경우의 수
- False Negative (FN) – 제2종 오류
- 실제 값은 ‘Positive’이지만, 모델이 ‘Negative’로 잘못 예측한 경우의 수
- True Positive (TP)
- 실제 값이 ‘Positive’이며, 모델도 ‘Positive’로 정확히 예측한 경우의 수
- True Negative (TN)
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# 실제값과 예측값을 임시로 구성
y_true = [1, 0, 1, 1, 0, 1] # y_test
y_pred = [0, 0, 1, 1, 0, 1] # 모델이 예측한 결과
r = confusion_matrix(y_true, y_pred) # 모델이 예측한 결과가 x축, 실제값이 y축에 있다
''' reuslt :
array([[2, 0], True Negative False Positive
[1, 3]]) False Negative True Positve
'''
ConfusionMatrixDisplay(confusion_matrix=r).plot()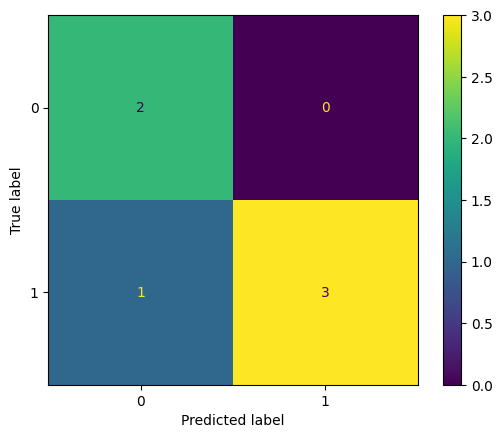
TN = r[0, 0]
FP = r[0, 1]
FN = r[1, 0]
TP = r[1, 1]4-2. 정확도(Accuracy)
- 전체 데이터중에, 정확하게 예측한 데이터의 수
(TN + TP) / (TN + FP + FN + TP) # 0.8333333333333334
# 기본이 되는 평가지표이므로 모델.score() 내장되어 있는 지표
from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred) # 0.83333333333333344-3. 정밀도(Precision)와 재현율(Recall)
- 정밀도(Precision)는 모델이 ‘Positive’라고 예측한 샘플들 중에서 실제로 ‘Positive’인 샘플의 비율
- 재현율(Recall)은 실제 ‘Positive’인 샘플들 중에서 모델이 ‘Positive’로 올바르게 예측한 샘플의 비율
정밀도
TP / (FP + TP) # 1.0
from sklearn.metrics import precision_score
precision_score(y_true, y_pred) # 1.0재현율
TP / (FN + TP) # 0.75
from sklearn.metrics import recall_score
recall_score(y_true, y_pred) #0.754-4. 임계값(Threshold)
임계값의 정의와 중요성
임계값은 모델의 예측을 분류하기 위한 기준점을 설정하는 값입니다. 이 값에 따라 모델이 데이터를 양성(Positive) 또는 음성(Negative)으로 분류합니다. 임계값의 설정은 모델의 성능 평가에 직접적인 영향을 미치며, 특히 불균형한 데이터셋에서 모델의 예측력을 조정하는 데 중요합니다.
재현율(Recall)과 정밀도(Precision)의 관계
재현율은 실제 양성 데이터 중 모델이 양성으로 올바르게 예측한 비율을, 정밀도는 모델이 양성으로 예측한 데이터 중 실제로 양성인 비율을 나타냅니다. 두 지표 모두 True Positive를 높이는 것을 목표로 하지만, 재현율은 False Negative를 줄이는 데, 정밀도는 False Positive를 줄이는 데 각각 더 큰 중점을 둡니다.
# 기본적인 경우 threshold = 0.5로 계산하나 상황에 따라 변경할 수 있습니다.
# 예측 확률과 값 연결
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.preprocessing import Binarizer
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt
# 데이터 만들기
X, y = make_classification(n_samples=150, n_features=2, n_informative=2, n_redundant=0, random_state=30)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True)
# 모델 학습
lr = LogisticRegression()
lr.fit(X_train, y_train)
pred_proba = lr.predict_proba(X_test)
pred = lr.predict(X_test)
#예측확률 array와 예측 결과값 array를 병합하여 예측확률과 결괏값을 한 번에 확인
pred_proba_result = np.concatenate([pred_proba, pred.reshape(-1,1)], axis=1)
print('두 개의 class 중 더 큰 확률을 클래스 값으로 예측\n', pred_proba_result[:])
# threshold 값 변경하기 - Binarizer
binarizer = Binarizer(threshold=0.3).fit(pred_proba)
pred_bin = binarizer.transform(pred_proba)[:, 1]
print(f'''
{binarizer.threshold, pred_bin}
정확도: {accuracy_score(y_test, pred)}
정밀도: {precision_score(y_test, pred)}
재현율: {recall_score(y_test, pred)}
''')
# precision,recall은 trade off관계, precision_recall_curve( )
precision, recall, th = precision_recall_curve(y_test, pred)
plt.xlabel('threadhold') #임계값
plt.ylabel('score')
plt.plot(th,precision[:len(th)],'red',linestyle = '--',label = 'precision')
plt.plot(th,recall[:len(th)],'blue',label = 'recall')
plt.legend()
plt.show()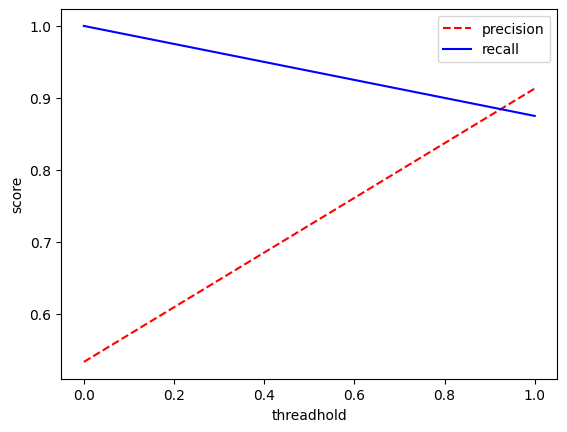
코드설명
1. 데이터 준비 및 모델 학습
make_classification을 사용하여 이진 분류를 위한 테스트 데이터를 생성합니다.train_test_split으로 데이터를 훈련 세트와 테스트 세트로 분리합니다.LogisticRegression모델을 사용하여 훈련 데이터에 대해 모델을 학습합니다.
2. 예측 확률과 결괏값 연결
predict_proba메소드로 얻은 예측 확률과predict메소드로 얻은 클래스 예측값을 병합합니다.
3. 임계값(Threshold) 조정
Binarizer를 사용하여 임계값을 조정함으로써 모델의 예측을 이진화합니다.- 임계값을 변경하면서 정밀도, 재현율 및 정확도(accuracy)를 계산하여 모델의 성능 변화를 관찰합니다.
4. 정밀도와 재현율의 트레이드오프(Trade-off)
- 정밀도와 재현율은 서로 반비례 관계에 있습니다.
precision_recall_curve함수를 사용하여 다양한 임계값에서의 정밀도와 재현율을 계산하고, 이를 그래프로 시각화합니다.
4-5. F1 Score(F-measure)
- F1 점수는 정밀도와 재현율의 조화 평균을 나타내므로, 정밀도와 재현율이 어느 한쪽으로 치우치지 않고 균형을 이룰 때 더 높은 값을 가집니다.
- 계산식 : F1 = 2×(precision×recall) / (precision+recall)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
(2 * (precision * recall)) / (precision + recall) # 0.8571428571428571- 계산된
0.8571428571428571이라는 F1 점수는 0과 1 사이의 값으로, 1에 가까울수록 모델의 성능이 뛰어나다는 것을 의미합니다. F1 점수가 높다는 것은 모델이 ‘Positive’ 클래스를 정확하게 예측하는 데 있어서 정밀도와 재현율 양쪽 모두에서 좋은 성능을 보이고 있음을 나타냅니다.
4-6. ROC 곡선과 AUC
AUC의 장점
- 척도 불변(Scale-Invariant)
- 모델의 예측값이 어떤 척도로 표현되어 있든 간에, AUC는 예측값의 순위 정보만을 사용하여 모델의 성능을 평가합니다. 이는 예측값의 절대적인 크기나 단위에 영향을 받지 않음을 의미합니다.
- 예를 들어, 확률 값이나 점수 등 다양한 형태로 예측값이 주어져도, 이 값들의 상대적인 크기(순위)만이 모델 성능 평가에 사용됩니다. 이러한 특성은 모델의 예측 성능을 척도에 구애받지 않고 일관된 기준으로 평가할 수 있게 합니다
- 분류 임계값 불변(Classification-Threshold-Invariant)
- AUC는 모델이 예측한 결과를 분류하는 데 사용되는 임계값의 변화에 따른 영향을 받지 않습니다. 이는 모델이 예측한 값에 대해 어떠한 임계값을 설정하더라도, 모델의 예측 품질을 일관되게 평가할 수 있음을 의미합니다.
ROC 곡선의 활용
- 다양한 임계값에서 모델의 성능 비교: ROC 곡선을 통해 다른 모델들을 여러 임계값에서 비교하여 최적의 모델을 선정합니다.
- 불균형 데이터셋의 성능 평가: 불균형한 클래스 분포를 가진 데이터셋에서 모델의 성능을 정확하게 평가합니다.
from sklearn.metrics import roc_auc_score
print(y_true) # [1, 0, 1, 1, 0, 1]
print(y_pred) # [0, 0, 1, 1, 0, 1]
roc_auc_score(y_true, y_pred) #0.875- ROC 곡선은 거짓 양성 비율(FPR)에 대한 참 양성 비율(TPR)의 곡선입니다. roc_auc_score는 이 곡선 아래의 면적을 계산합니다. 면적이 1에 가까울수록 모델의 성능이 우수하고, 0.5에 가까울수록 무작위 분류와 같습니다.
from sklearn.metrics import RocCurveDisplay
RocCurveDisplay.from_predictions(y_true, y_pred)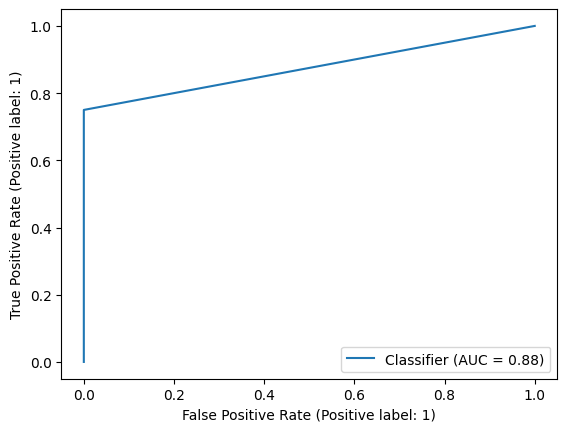
sklearn.metrics모듈에서RocCurveDisplay클래스를 가져와서, 실제 라벨(y_true)과 예측 라벨(y_pred)을 사용하여 ROC 곡선을 표시합니다.from_predictions메서드는 실제 값과 예측 값을 바탕으로 ROC 곡선을 그리고, 이를 시각화하는 데 사용합니다.
from sklearn.metrics import classification_report
print(classification_report(y_true, y_pred))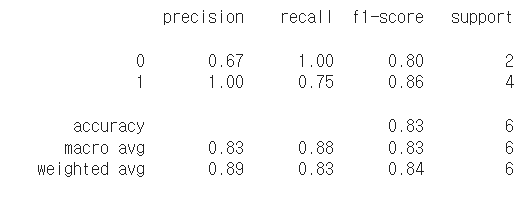
classification_report함수는 분류 모델의 성능을 평가하기 위한 도구로 사용됩니다. 이 함수는 모델이 예측한 값과 실제 타겟값을 비교하여 여러 가지 성능 지표를 계산하고 이를 보고서 형태로 제공합니다.
5. 평균 점수 계산 방법
5-1. Macro 평균
- 정의: 모든 클래스에 동등한 중요도를 부여하여 각 클래스별 성능 지표를 먼저 계산한 후, 이들의 평균을 취하는 방식입니다.
- 적용 상황: 클래스 간 불균형이 클 때 유용하며, 소수 클래스의 성능이 중요할 때 사용합니다.
- 장점: 모든 클래스를 동일하게 취급하여 소수 클래스의 성능이 결과에 큰 영향을 미칩니다.
- 단점: 빈도가 높은 클래스와 낮은 클래스가 동일하게 취급되어, 모델이 실제로 더 자주 접하는 클래스에 대한 성능이 과소평가될 수 있습니다.
5-2. Weighted 평균
- 정의: 각 클래스의 샘플 개수에 비례하여 가중치를 적용한 평균을 계산하는 방식입니다. 즉, 각 클래스별 성능 지표에 클래스 내 샘플 수를 가중치로 곱한 후 합산합니다.
- 적용 상황: 클래스 불균형이 있을 때 유용하며, 각 클래스의 샘플 크기를 반영하여 평가하고 싶을 때 사용합니다.
- 장점: 샘플 수가 많은 클래스의 성능이 전체 평가에 더 큰 영향을 미칩니다. 이는 더 현실적인 모델 성능 평가를 제공할 수 있습니다.
- 단점: 소수 클래스의 성능이 전체 평가에 미치는 영향이 줄어들어, 중요한 소수 클래스를 간과할 위험이 있습니다.
5-3. Micro 평균
- 정의: 전체 데이터셋에 대해 TP, TN, FP, FN을 집계한 후, 이를 기반으로 성능 지표를 계산합니다. 이 방식은 각 샘플에 동일한 가중치를 부여합니다.
- 적용 상황: 각 샘플의 정확한 분류가 중요할 때 또는 클래스 간 성능의 균형을 중시할 때 사용합니다.
- 장점: 전체 데이터셋에 대한 정밀한 성능 평가를 제공하며, 모든 예측을 동등하게 취급합니다.
- 단점: 클래스 불균형이 성능 평가에 미치는 영향을 직접적으로 해결하지는 않습니다. 그러나, 각 샘플의 정확도에 중점을 둔다는 점에서 이는 일부 상황에서는 장점으로 작용할 수 있습니다.