백준 17213번: 과일 서리 – Python(파이썬)

백준 17213번 과일서리에 대해서 알아보겠습니다. 이 문제는 1) 수학, 2) 다이나믹 프로그래밍, 3) 조합론의 알고리즘으로 분류되어있습니다. 이 중에서 다이나믹 프로그래밍을 이용하여 해결하였습니다.

문제 설명

• N개의 종류에서 M개를 선택하는 경우의 수를 구하는 문제입니다. 이때 N개의 종류는 각각 최소 1번 이상 선택되어야 합니다.
• 입력이 N<=10, M<=30 이므로 2차원 dp를 이용하여 풀어도 됩니다.
• https://www.acmicpc.net/problem/17213

접근법

• 중복 조합
  • nHr=(n−1+r)C(n-1) 을 이용합니다.
  • M의 과일의 개수가 있을 때 모든 종류의 과일을 적어도 1개는 훔쳐야 하니, M-N개의 과일을 중복 조합할 수 있습니다.
  • 따라서 nHm-n = (n-1+(m-n))C(n-1) = (m-1)C(n-1) 이 됩니다.
• 다이나믹 프로그래밍
  • n=1 즉 과일의 종류가 1개라고 가정하겠습니다. 그러면 m 과일의 개수와 상관없이 경우의 수는 1가지 입니다.
  • n=2 때는 과일의 종류가 2개입니다. 사과랑 배가 있다고 가정하겠습니다.
    • n<m : 과일의 개수가 종류보다 작다면 훔칠 수 없습니다.
    • n>=m : 과일의 종류가 2개일 때는 과일을 하나 선택하면 나머지 과일은 자동으로 정해집니다.
  • 따라서 하나의 그룹의 개수가 정해지면, 나머지 2개의 그룹이 가져갈 양이 자동으로 정해집니다.
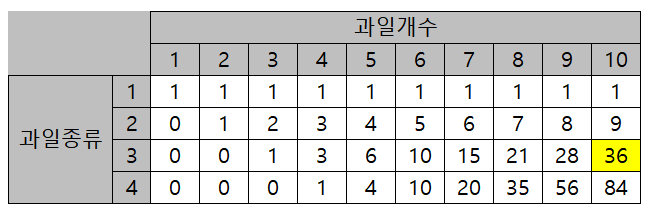
  • 즉 점화식은 다음과 같이 써집니다.
    • i는 사용할 수 있는 과일의 종류 수, j는 훔치려는 과일의 개수를 나타냅니다.
    • dp[i][j] = dp[i][j – 1] + dp[i – 1][j – 1]: 이는 두 가지 경우를 고려한 것입니다.
    • dp[i][j – 1]: i종류의 과일을 사용하여 (j-1)개의 과일을 이미 훔친 경우에, 1개를 더 훔쳐 j개가 되는 경우입니다.
    • dp[i – 1][j – 1]: i종류의 과일 중에서 새로운 종류를 사용하여 j개를 훔치는 경우의 수입니다. 이는 사과, 바나나, 오렌지가 있을 때 j-1개로 사과와 바나나의 조합으로 만든 경우의 수(dp[i-1][j-1])에 오렌지를 추가하는 경우입니다.

백준 정답 코드

n=int(input())
m=int(input())
#dp배열 선언
dp = [[0]*m for i in range(n)]
#과일종류가 1개일 때는 어떻게 골라도 1개의 경우의 수
dp[0] = [1]*m
for i in range(1,n) :
	#print("\n".join(map(str,dp)))
	dp[i][i] = 1 #과일종류 2개 중에서 2개 고를 경우의 수 {2} = 1
	for j in range(i+1,m) :
		dp[i][j] = dp[i-1][j-1]+dp[i][j-1]
        
print(dp[-1][-1])