Python을 이용한 1753번 : 물건팔기에 대해서 포스팅하겠습니다. 1753번은 그래프 이론,데이크스트라(다익스트라),최단 경로로 분류되는 문제입니다.
1. 1753번 문제설명
입력
- 정점의 개수 V와 간선의 개수 E가 주어집니다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000)
- 시작 정점의 번호 K가 주어집니다. (1 ≤ K ≤ V)
- E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 주어집니다. 이는 정점 u에서 정점 v로 가는 가중치 w인 간선이 존재함을 나타냅니다.
목표
- 주어진 시작점 K로부터 다른 모든 정점으로의 최단 경로를 구합니다. 모든 간선의 가중치는 10 이하의 자연수입니다.
출력
- 첫째 줄부터 V개의 줄에 걸쳐 i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력합니다.
- 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 “INF”를 출력합니다.
2. 1753번 접근방법
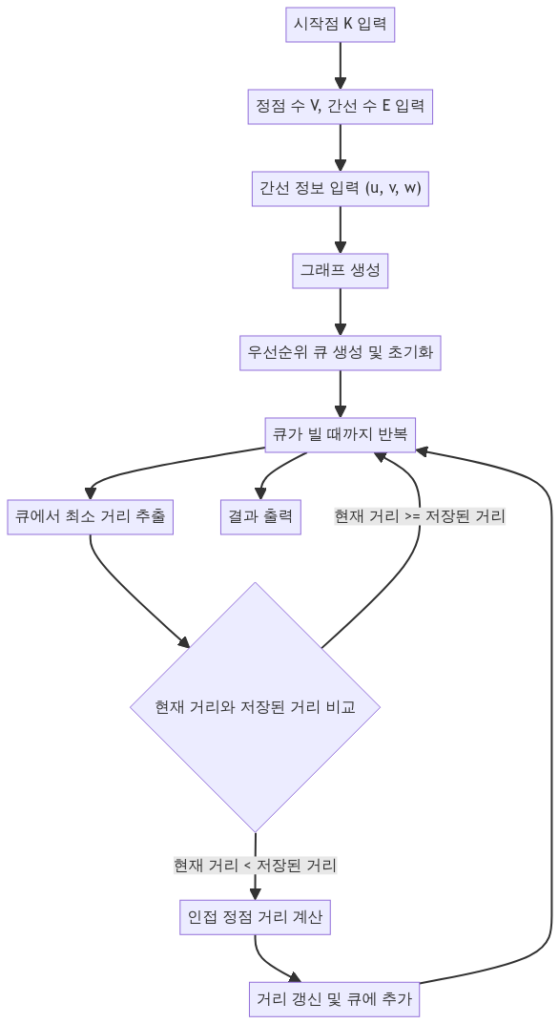
다익스트라 알고리즘
- 다익스트라 알고리즘은 가중치가 있는 그래프에서 하나의 정점으로부터 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다. 이 알고리즘은 우선순위 큐를 사용하여 현재까지 발견된 최단 경로를 계속해서 갱신하며, 방문한 정점의 최단 거리를 확정합니다. 시간 복잡도는 O(E log V)입니다.
- 시작 정점으로부터 다른 모든 정점으로의 최단 경로를 찾기 위해 다익스트라 알고리즘을 구현합니다. 초기화 단계에서는 시작 정점의 거리를 0으로 설정하고, 나머지 정점의 거리를 무한대로 설정합니다. 우선순위 큐를 사용하여 현재 정점에서 인접한 정점으로의 거리를 갱신하고, 갱신된 거리가 더 짧으면 큐에 삽입합니다.
우선순위 큐와 힙 자료구조
- 우선순위 큐는 가장 우선순위가 높은 요소를 효율적으로 추출할 수 있는 자료구조입니다. 파이썬에서는
heapq모듈을 사용하여 최소 힙으로 구현할 수 있습니다. 힙은 이진 트리 구조로서 삽입과 삭제 연산이 O(log N)의 시간 복잡도를 가집니다.
3. 1753번 구현
3-1. 1753번 코드
Python
from sys import stdin
import heapq
# 정점(V)과 간선(E)의 개수를 입력받음
V, E = map(int, stdin.readline().split())
# 시작 정점의 번호(K)를 입력받음
K = int(stdin.readline())
# 간선 정보를 리스트로 입력받음
nums = list(map(lambda a: list(map(int, a.split())), stdin.readlines()))
# 다익스트라 알고리즘 정의
def dijkstra(graph, K, result):
# 우선순위 큐를 생성하고 시작 정점을 큐에 추가
queue = [(0, K)]
while queue:
# 큐에서 가장 작은 거리를 가진 정점을 추출
current_distance, u = heapq.heappop(queue)
# 현재 정점의 저장된 거리보다 크면 무시
if result[u - 1] < current_distance:
continue
# 인접한 정점들을 확인하여 거리 갱신
for v, weight in graph[u]:
distance = current_distance + weight
# 갱신된 거리가 더 짧으면 업데이트하고 큐에 추가
if distance < result[v - 1]:
result[v - 1] = distance
heapq.heappush(queue, (distance, v))
# 그래프를 인접 리스트 형태로 생성
graph = [[] for _ in range(V + 1)]
for (u, v, w) in nums:
graph[u].append((v, w))
# 결과 리스트를 무한대로 초기화하고, 시작 정점의 거리를 0으로 설정
result = [float('inf') for i in range(V)]
result[K - 1] = 0
# 다익스트라 알고리즘 실행
dijkstra(graph, K, result)
# 결과를 출력, 무한대는 'INF'로 변환하여 출력
print("\n".join(map(lambda a: 'INF' if a == float('inf') else str(a), result)))