Python을 이용한 2096번 : 물건팔기에 대해서 포스팅하겠습니다. 2096번은 다이나믹 프로그래밍, 슬라이딩 윈도우알고리즘로 분류되는 문제입니다.
1. 2096번 문제설명
입력
- 첫째 줄: 게임의 줄 수 N (1 ≤ N ≤ 100,000)
- 다음 N개의 줄: 각 줄에 0 이상 9 이하의 숫자 3개
목표
- 첫 줄에서 시작하여 마지막 줄까지 내려가면서 얻을 수 있는 최대 점수와 최소 점수를 계산
- 이동할 수 있는 경로는 바로 아래 줄의 숫자 또는 바로 아래 줄의 양옆에 있는 숫자만 가능
출력
- 첫째 줄: 얻을 수 있는 최대 점수와 최소 점수를 공백으로 구분하여 출력
2. 2096번 접근방법
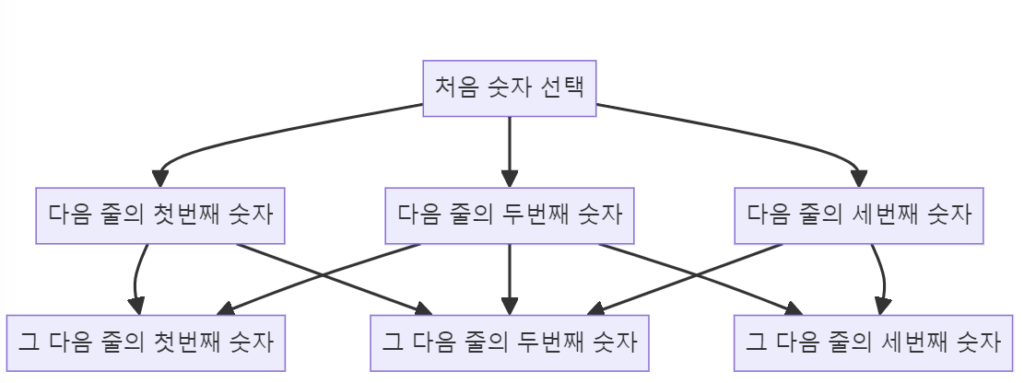
- 동적 계획법 초기화
- 동적 계획법(Dynamic Programming, DP)을 사용하여 문제를 해결하기 위해 초기 상태를 설정합니다.
max_dp와min_dp라는 두 개의 2차원 리스트를 초기화하여 각 줄에서 최대 및 최소 점수를 저장합니다. 초기화 단계에서는 첫 번째 줄의 숫자들을 그대로 최대 및 최소 점수로 설정합니다. 이를 통해 첫 번째 줄에서 시작하는 각 숫자에 대한 초기 점수를 설정합니다.
- 동적 계획법(Dynamic Programming, DP)을 사용하여 문제를 해결하기 위해 초기 상태를 설정합니다.
- 동적 계획법을 통한 최대 및 최소 점수 계산
- 각 줄에서 가능한 이동 경로를 고려하여 최대 및 최소 점수를 계산합니다.
max_dp와min_dp리스트를 이용하여 현재 줄에서 얻을 수 있는 최대 및 최소 점수를 업데이트합니다. 이를 위해 이전 줄에서 가능한 점수들 중 최대값과 최소값을 각각 선택하여 현재 줄의 숫자와 더해줍니다. 이 과정을 반복함으로써 최종 줄까지의 최대 및 최소 점수를 계산합니다.
- 각 줄에서 가능한 이동 경로를 고려하여 최대 및 최소 점수를 계산합니다.
3. 2096번 구현
3-1. 2096번 코드
Python
from sys import stdin
# 게임의 줄 수 N을 입력받음
n = int(stdin.readline())
# 각 줄에 대해 숫자를 입력받고 최대/최소 점수를 계산
for i in range(0, n):
# 현재 줄의 숫자들을 리스트로 변환하여 입력받음
nums = list(map(int, stdin.readline().split()))
# 첫 번째 줄인 경우 초기화 작업 수행
if i == 0:
# 최대 점수를 저장할 2차원 리스트 초기화 (2개의 줄, 각 줄에 3개의 값)
max_dp = [[0 for j in range(3)] for i in range(2)]
# 최소 점수를 저장할 2차원 리스트 초기화 (초기값을 무한대로 설정)
min_dp = [[float('inf') for j in range(3)] for i in range(2)]
# 첫 번째 줄의 숫자들을 그대로 최대/최소 점수로 설정
max_dp[0] = nums[::]
min_dp[0] = nums[::]
else:
# 현재 줄의 인덱스를 기준으로 반대 줄의 인덱스를 계산
reverse = 0 if i % 2 == 1 else 1
# 최대 점수를 계산하여 현재 줄에 업데이트
max_dp[i % 2][0] = nums[0] + max(max_dp[reverse][0], max_dp[reverse][1])
max_dp[i % 2][1] = nums[1] + max(max_dp[reverse][0], max_dp[reverse][1], max_dp[reverse][2])
max_dp[i % 2][2] = nums[2] + max(max_dp[reverse][1], max_dp[reverse][2])
# 최소 점수를 계산하여 현재 줄에 업데이트
min_dp[i % 2][0] = nums[0] + min(min_dp[reverse][0], min_dp[reverse][1])
min_dp[i % 2][1] = nums[1] + min(min_dp[reverse][0], min_dp[reverse][1], min_dp[reverse][2])
min_dp[i % 2][2] = nums[2] + min(min_dp[reverse][1], min_dp[reverse][2])
# 마지막 줄의 최대 점수와 최소 점수를 출력
print(max(max_dp[(n - 1) % 2]), min(min_dp[(n - 1) % 2]))
3-2. 트러블 슈팅
처음에는 max_dp와 min_dp를 입력의 개수만큼 만들어줬습니다. 그렇게 했더니 메모리 제한이 걸리게 되었습니다. 문제의 조건은 아래와 같았습니다.
- 메모리 제한: 4MB (4,000,000 바이트)
- 최대 입력 크기: 한 줄에 3개의 숫자가 주어지며, 최대 100,000줄까지 입력이 주어질 수 있음
메모리를 계산해보면
- 한 줄의 메모리 사용량:
- 3개의 숫자 × 4바이트 = 12바이트
- 최대 줄 수:
- 100,000줄
- 총 메모리 사용량:
- 100,000줄 × 12바이트 = 1,200,000바이트 (약 1.2MB)
- max_dp: 1,200,000바이트 (약 1.2MB)
min_dp: 1,200,000바이트 (약 1.2MB)
입력 데이터: 1,200,000바이트 (약 1.2MB) - 총 3.6MB에 시스템에서 사용하는 메모리를 포함하면 4MB를 초과할 수 있게 됩니다.
따라서 max_dp와 min_dp 배열을 두 줄만 사용하여 현재 줄과 이전 줄의 값을 저장하도록 하였습니다.