Python을 이용한 17070번 : 파이프 옮기기 1 에 대해서 포스팅하겠습니다. 17070번은 다이나믹 프로그래밍, 그래프 이론, 그래프 탐색의 알고리즘으로 분류되는 문제입니다.
17070번 문제설명
- 조건
- 가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다.
- 파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
- 입력
- 첫째 줄에 집의 크기 N(3 ≤ N ≤ 16)이 주어진다. 둘째 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈 칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈 칸이다.
- 출력
- 첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다. 방법의 수는 항상 1,000,000보다 작거나 같다.
17070번 접근방법
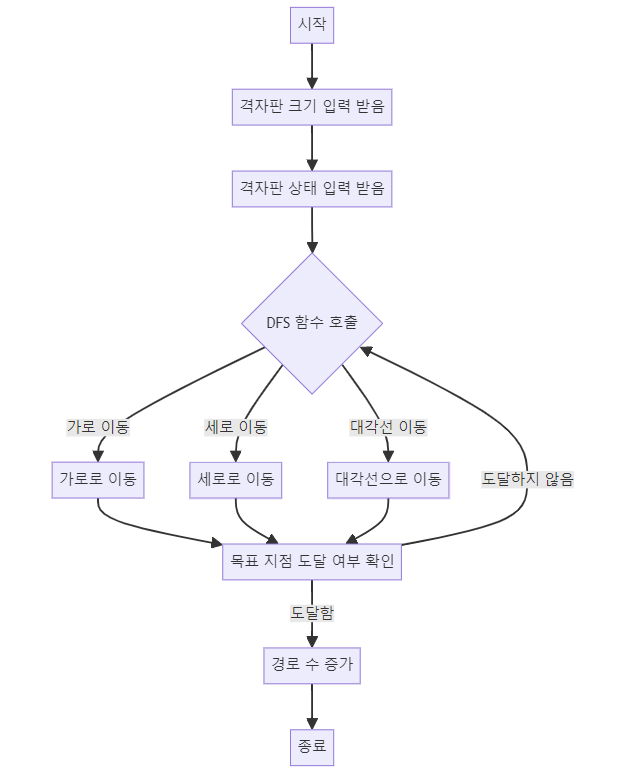
1. 17070번의 DFS 탐색
- 시작 지점과 방향 설정: 처음에 파이프는 (1, 1)과 (1, 2)를 차지하며, 방향은 가로입니다. 따라서 DFS 탐색은 (0, 1) 위치에서 가로 방향으로 시작합니다.
- 경로 탐색:
- 가로 방향(
rotation = 0)인 경우, 파이프는 오른쪽 또는 대각선 아래로 이동할 수 있습니다. - 세로 방향(
rotation = 1)인 경우, 파이프는 아래쪽 또는 대각선 아래로 이동할 수 있습니다. - 대각선 방향(
rotation = 2)인 경우, 파이프는 오른쪽, 아래쪽 또는 대각선 아래로 이동할 수 있습니다.
- 가로 방향(
- 이동 조건 확인:
- 범위 확인: 파이프의 이동이 격자판의 범위를 벗어나지 않는지 확인합니다.
- 벽 확인: 이동하려는 칸이 벽이 아닌지, 특히 대각선 이동 시 인접한 칸이 벽인지 확인합니다.
- 목표 지점 도달 여부 확인: 파이프 한쪽 끝이 (N, N) 위치에 도달했는지 확인합니다. 도달한 경우, 경로 수를 증가시킵니다.
- 재귀적 탐색: 가능한 모든 방향으로 파이프를 이동시켜 재귀적으로 탐색을 계속합니다.
2. 17070번의 DP 점화식
2-1. DP 점화식 도출 과정:
- 상태 정의: DP[r][c][d]를 (r, c) 위치에서 파이프가 d 방향(0: 가로, 1: 세로, 2: 대각선)으로 놓일 수 있는 배치 방법의 수라고 정의합니다.
- 초기 상태: (0, 1) 위치에서 파이프는 가로 방향으로만 놓일 수 있으므로, DP[0][1][0] = 1로 초기화합니다. 다른 상태는 0으로 초기화합니다.
- 전이(점화식):
- 가로 방향(d=0)으로 놓인 파이프를 (r, c+1)로 이동시키기 위해서는 이전 상태가 가로 또는 대각선이어야 합니다.
DP[r][c+1][0] += DP[r][c][0] + DP[r][c][2]
- 세로 방향(d=1)으로 놓인 파이프를 (r+1, c)로 이동시키기 위해서는 이전 상태가 세로 또는 대각선이어야 합니다.
DP[r+1][c][1] += DP[r][c][1] + DP[r][c][2]
- 대각선 방향(d=2)으로 놓인 파이프를 (r+1, c+1)로 이동시키기 위해서는 이전 상태가 가로, 세로, 또는 대각선이어야 합니다.
DP[r+1][c+1][2] += DP[r][c][0] + DP[r][c][1] + DP[r][c][2]
- 가로 방향(d=0)으로 놓인 파이프를 (r, c+1)로 이동시키기 위해서는 이전 상태가 가로 또는 대각선이어야 합니다.
- 벽 확인: 이동하려는 위치에 벽이 있으면 이동할 수 없습니다. 따라서 해당 위치가 모두 빈 칸인지 확인해야 합니다.
2-2. 점화식 도출을 위한 생각 과정:
- 경우의 수 분할: 파이프가 각 방향으로 이동할 때 고려해야 할 이전 상태를 분리해서 생각합니다.
- 경계 조건: 파이프가 격자판 밖으로 나가거나 벽을 만나는 경우를 배제합니다.
- 중복 계산 방지: 각 위치와 방향별로 이동 가능한 경로의 수를 계산함으로써 중복 계산을 방지합니다.
2-3. 점화식의 의미:
- DP[r][c][0]: (r, c)에 가로 방향으로 파이프가 놓일 수 있는 모든 경우의 수.
- DP[r][c][1]: (r, c)에 세로 방향으로 파이프가 놓일 수 있는 모든 경우의 수.
- DP[r][c][2]: (r, c)에 대각선 방향으로 파이프가 놓일 수 있는 모든 경우의 수.
3. 17070번 코드
Python
#https://www.acmicpc.net/problem/17070
from sys import stdin
# N: 격자판의 크기 (N x N)
n = int(stdin.readline())
# maps: 격자판의 상태를 나타내는 2차원 리스트. 0은 빈 칸, 1은 벽
maps = [list(map(int, stdin.readline().split())) for i in range(n)]
# path: 파이프가 (N, N) 위치로 이동할 수 있는 방법의 총 수
path = 0
# dfs 함수: 파이프의 현재 위치와 상태를 기준으로 이동 가능한 경로를 탐색하는 함수
def dfs(i, j, rotation):
global path, maps
# 이동이 격자판 범위를 벗어나거나, 벽(1)을 만나면 탐색 중단
if not(0 <= i < n) or not(0 <= j < n) or maps[i][j] == 1:
return
# 대각선 이동 중 벽이 있으면 이동 불가, 탐색 중단
if rotation == 2 and (maps[i-1][j] == 1 or maps[i][j-1] == 1):
return
# (N, N) 위치에 도달하면 경로 수 증가 후 탐색 중단
if i == n-1 and j == n-1:
path += 1
return
# 파이프가 가로 방향일 때: 오른쪽(가로) 또는 대각선으로 이동 가능
if rotation == 0:
dfs(i, j+1, 0) # 오른쪽으로 가로 이동
dfs(i+1, j+1, 2) # 대각선으로 이동
# 파이프가 세로 방향일 때: 아래(세로) 또는 대각선으로 이동 가능
if rotation == 1:
dfs(i+1, j, 1) # 아래로 세로 이동
dfs(i+1, j+1, 2) # 대각선으로 이동
# 파이프가 대각선 방향일 때: 모든 방향으로 이동 가능 (가로, 세로, 대각선)
if rotation == 2:
dfs(i, j+1, 0) # 오른쪽으로 가로 이동
dfs(i+1, j, 1) # 아래로 세로 이동
dfs(i+1, j+1, 2) # 대각선으로 이동
# N이 16이 아닌 경우에 대한 예외 처리입니다.
if n != 16:
# 특정 조건에서는 경로가 존재하지 않으므로 0을 출력합니다.
if (maps[0][2]==1 or (maps[n-1][n-2] == 1 and maps[n-2][n-1] == 1)):
print(0)
else:
# DFS 탐색 시작점: 처음 파이프 위치(0, 1)와 방향(가로)
dfs(0, 1, 0)
# 최종 계산된 이동 경로의 수 출력
print(path)
else:
# N이 16인 경우, 동적 프로그래밍을 사용하여 문제를 해결합니다.
dp = [[[0] * 3 for _ in range(n)] for _ in range(n)]
dp[0][1][0] = 1 # 초기 조건 설정
for r in range(n):
for c in range(n):
# 가로로 이동하는 경우의 수를 계산합니다.
if c + 1 < n and maps[r][c + 1] == 0:
dp[r][c + 1][0] += dp[r][c][0] + dp[r][c][2]
# 세로로 이동하는 경우의 수를 계산합니다.
if r + 1 < n and maps[r + 1][c] == 0:
dp[r + 1][c][1] += dp[r][c][1] + dp[r][c][2]
# 대각선으로 이동하는 경우의 수를 계산합니다.
if r + 1 < n and c + 1 < n and maps[r + 1][c] == 0 and maps[r][c + 1] == 0 and maps[r + 1][c + 1] == 0:
dp[r + 1][c + 1][2] += dp[r][c][0] + dp[r][c][1] + dp[r][c][2]
# 최종적으로 (N, N)에 도달하는 모든 경우의 수를 합하여 출력합니다.
print(sum(dp[n - 1][n - 1]))