Python을 이용한 2485번 : 예산에 대해서 포스팅하겠습니다. 2485번은 수학, 정수론, 유클리드, 호제법으로 분류되는 문제입니다.
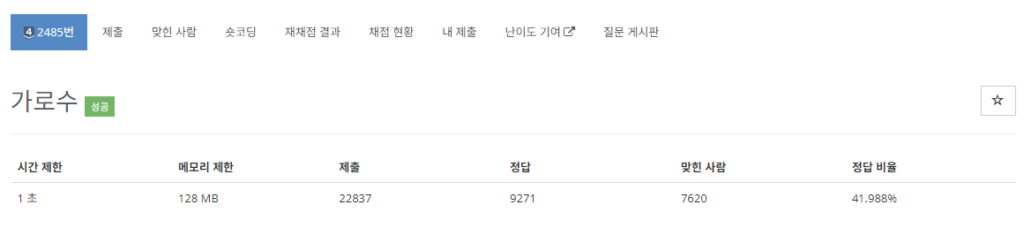
1. 2485번 문제설명
- 입력:
- 첫 번째 줄에는 심어져 있는 가로수의 수 N이 주어집니다. (3 ≤ N ≤ 100,000)
- 두 번째 줄부터 N개의 줄에 걸쳐 각 가로수의 위치가 주어집니다. 위치는 1 이상 1,000,000,000 이하의 양의 정수이며, 가로수의 위치는 오름차순으로 주어집니다.
- 목표:
- 모든 가로수가 같은 간격이 되도록 하기 위해 추가로 필요한 가로수의 최소 수를 찾습니다.
- 출력:
- 첫째 줄에 추가로 필요한 가로수의 수를 출력합니다.
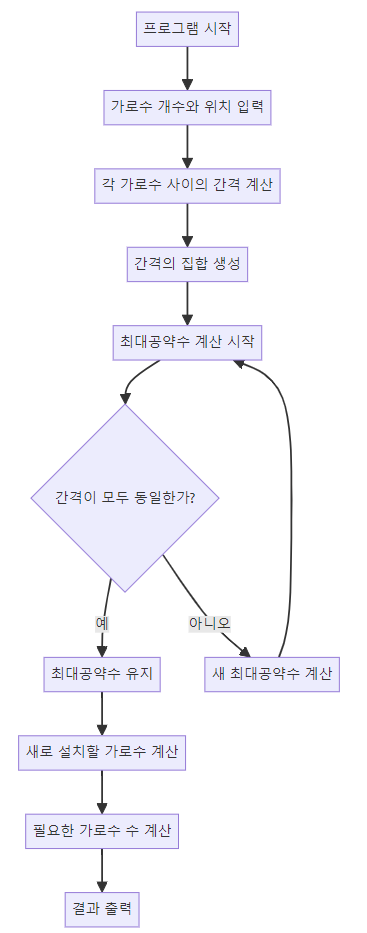
2. 2485번 접근방법
- 이 문제에서 중요한 것은 총 예산액 내에서 가능한 한 많은 요청을 만족시키는 것이므로, 이분 탐색 과정에서 총 예산액을 초과하지 않는 선에서 최대한의 상한액을 찾는 것입니다.
- 이분 탐색을 사용함으로써, O(NlogM)의 시간 복잡도로 문제를 해결할 수 있으며, 이는 대부분의 입력 크기에 대해 충분히 효율적입니다.
3. 2485번 구현
1. 입력 처리
표준 입력을 사용하여 가로수의 개수와 위치 정보를 받습니다. 입력값은 정수로 변환되고 리스트에 저장됩니다.
2. 간격 계산
연속된 가로수 사이의 간격을 계산하여 집합에 저장함으로써 중복된 간격을 제거합니다.
가로수 사이의 간격을 계산하여 집합에 저장하는 이유는 모든 가로수가 일정한 간격으로 배치되어야 함을 보장하기 위해서입니다. 예를 들어 가로수가 3개 있고 위치가 각각 1m, 4m, 10m에 위치해 있다면, 이 가로수들 사이의 간격은 3m와 6m입니다. 이 경우, 간격을 일관되게 하려면 어떤 고정 간격을 설정하여 모든 가로수가 그 간격을 따라야 합니다. 여기서 최대공약수의 개념이 도입됩니다.
3. 최대공약수 계산
집합에 저장된 간격들의 최대공약수를 계산합니다. 이 최대공약수는 후에 새로운 가로수를 설치할 간격의 기준이 됩니다.
최대공약수(Greatest Common Divisor, GCD)는 두 개 이상의 정수의 공통된 최대의 약수를 의미합니다. 각 간격의 최대공약수를 구하는 이유는 최소한의 추가 가로수를 설치하기 위해 가장 큰 단위의 공통 간격을 찾기 위해서입니다. 최대공약수가 크면 클수록 추가로 설치해야 할 가로수의 수는 줄어듭니다.
예를 들어, 가로수가 1m, 4m, 10m에 설치되어 있을 때 간격은 3m와 6m입니다. 이 간격들의 최대공약수는 3입니다. 이는 가로수를 최소 3m 간격으로 설치할 수 있다는 것을 의미하며, 이 간격을 유지하기 위해 필요한 최소한의 추가 가로수를 계산할 수 있습니다. 1m와 4m 사이에는 추가 가로수가 필요 없지만, 4m와 10m 사이에는 3m 간격을 유지하기 위해 7m 지점에 가로수 한 그루를 추가로 설치해야 합니다.
4. 추가 가로수 계산
각 간격에 대해 최대공약수를 이용하여 필요한 추가 가로수의 수를 계산합니다. 이는 간격을 최대공약수로 나눈 후 1을 빼줌으로써 이루어집니다.
3-1. 2485번 코드
# https://www.acmicpc.net/problem/2485
from sys import stdin
import math
# 표준 입력으로부터 가로수의 개수(n)와 가로수의 위치를 입력받습니다.
n = int(stdin.readline())
street_trees = list(map(int, stdin.read().splitlines()))
# 각 가로수 사이의 간격을 저장할 집합입니다. 집합을 사용하는 이유는 중복된 간격을 제거하기 위해서입니다.
nums = set()
# 첫 번째 for문: 각 가로수 사이의 간격을 계산하고, 그 값을 nums 집합에 추가합니다.
for i in range(1, n):
# street_trees[i] - street_trees[i-1]는 연속된 가로수 사이의 거리를 의미합니다.
nums.add(street_trees[i] - street_trees[i-1])
# 각 간격의 최대공약수를 구하는 과정입니다. 이 최대공약수는 새로운 가로수를 설치할 간격의 기준이 됩니다.
max_divide = None
for distance in nums:
if max_divide is None:
# 처음 비교 대상인 distance를 max_divide에 초기화합니다.
max_divide = distance
else:
# 기존의 max_divide와 새로운 distance의 최대공약수를 구하여 max_divide를 갱신합니다.
max_divide = math.gcd(max_divide, distance)
# 추가로 설치해야 하는 가로수의 개수를 구하는 과정입니다.
result = 0
for i in range(1, n):
# 연속된 가로수 사이의 간격을 temp 변수에 저장합니다.
temp = street_trees[i] - street_trees[i-1]
# 만약 이 간격이 최대공약수보다 크다면, 추가로 가로수를 설치해야 합니다.
if temp > max_divide:
# 추가로 설치해야 할 가로수의 수는 (간격 / 최대공약수 - 1)입니다.
# 예를 들어 간격이 12이고 최대공약수가 4라면, 사이에 2개의 추가 가로수가 필요합니다 (12 / 4 - 1 = 2).
result += temp // max_divide - 1
# 최종적으로 계산된 결과를 출력합니다.
print(result)