Python을 이용한 2018번 : 예산에 대해서 포스팅하겠습니다. 2018번은 수학, 두 포인터으로 분류되는 문제입니다.
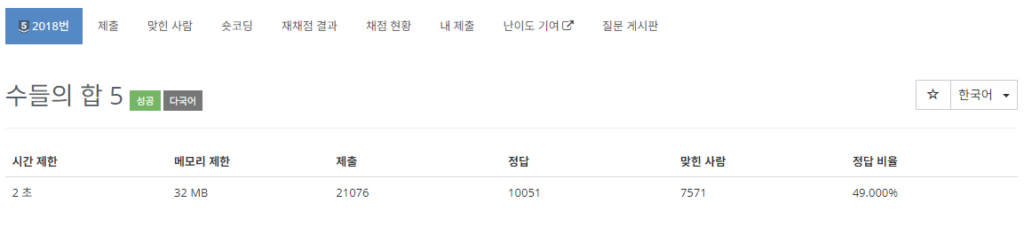
1. 2018번 문제설명
- 입력
- 자연수 N (1 ≤ N ≤ 10,000,000)
- 목표
- 주어진 자연수 N을 연속된 자연수들의 합으로 표현할 수 있는 모든 경우의 수를 찾아야 합니다. 예를 들어, N=15인 경우 가능한 표현은 15, 7+8, 4+5+6, 1+2+3+4+5로 총 4가지 방법이 있습니다.
- 출력
- 입력된 자연수 N을 연속된 자연수의 합으로 나타낼 수 있는 가지수를 출력합니다. 예를 들어, N=15일 경우 출력값은 4가 됩니다.
2. 2018번 접근방법
- 이 문제에서 중요한 것은 총 예산액 내에서 가능한 한 많은 요청을 만족시키는 것이므로, 이분 탐색 과정에서 총 예산액을 초과하지 않는 선에서 최대한의 상한액을 찾는 것입니다.
- 이분 탐색을 사용함으로써, O(NlogM)의 시간 복잡도로 문제를 해결할 수 있으며, 이는 대부분의 입력 크기에 대해 충분히 효율적입니다.
3. 2018번 구현
- 변수 설명
- left: 연속된 수열의 시작 지점
- right: 연속된 수열의 끝 지점
- temp: 현재까지의 연속된 수의 합
- count: 가능한 연속된 수열의 수
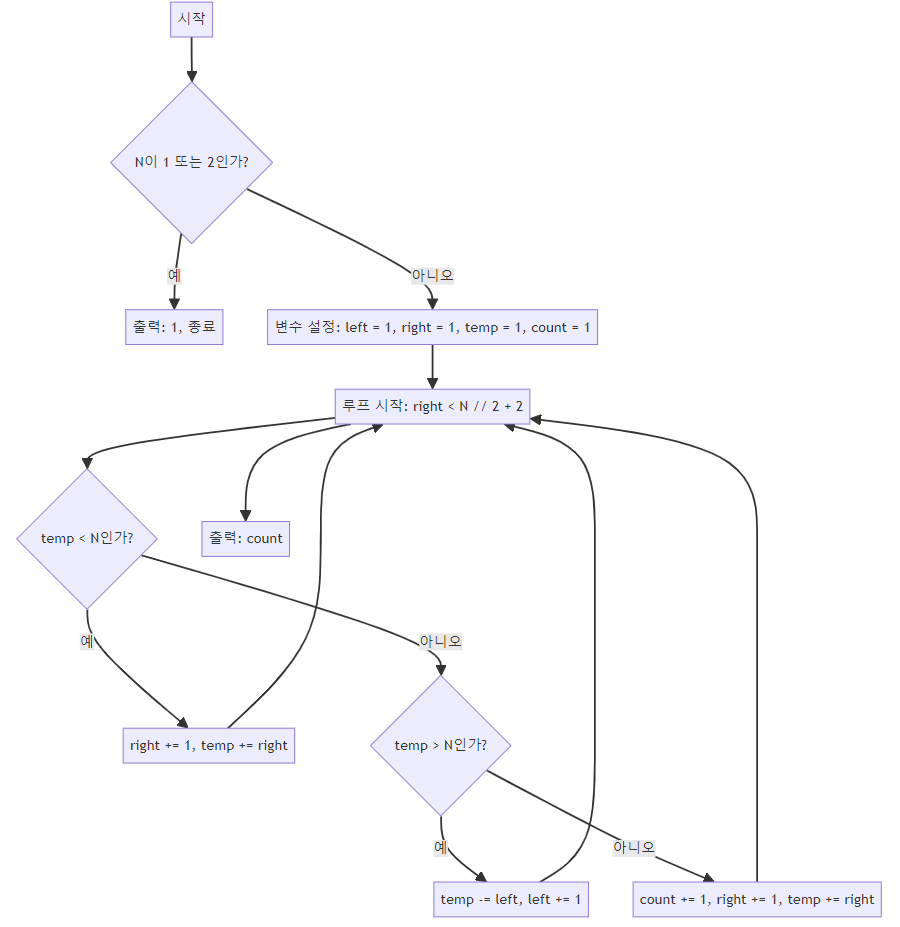
left와right를 이용하여 구간을 조절하며 합을 계산합니다. 초기에는left,right,temp모두 1로 설정하고, 자기 자신만으로 수를 만들 수 있는 경우를count에 미리 반영합니다. - 조건 분기
- temp < N: 현재 합이 N보다 작으면
right를 하나 증가시켜 합에 추가합니다. - temp > N: 현재 합이 N보다 크면
left를 하나 증가시켜 합에서 제거합니다. - temp == N: 현재 합이 N과 동일하면 가능한 수열을 찾았으므로
count를 증가시키고,right를 증가시켜 다음 가능성을 탐색합니다.
left와right를 조절하며 가능한 모든 수열을 찾습니다. - temp < N: 현재 합이 N보다 작으면
- 종료 조건
- right < N // 2 + 2:
right가 N의 절반보다 크게 될 때까지 반복합니다.
- right < N // 2 + 2:
3-1. 2018번 코드
Python
import sys
N = int(sys.stdin.readline())
left, right = 1, 1 # 연속된 자연수의 시작과 끝
temp = 1 # 현재 합
count = 1 # 초기값은 자기 자신 N
# N이 1 또는 2인 경우, 연속된 수로 표현하는 방법은 자기 자신 밖에 없음
if N == 1 or N == 2:
print(1)
sys.exit()
# right가 N의 절반 넘어갈 때까지 반복
while right < N // 2 + 2:
if temp < N: # 현재 합이 N보다 작으면
right += 1 # 끝 점을 오른쪽으로 이동
temp += right # 새로운 right 값을 합에 추가
elif temp > N: # 현재 합이 N보다 크면
temp -= left # 시작 점의 값을 합에서 빼고
left += 1 # 시작 점을 오른쪽으로 이동
else: # 합이 N과 같으면
count += 1 # 카운트 증가
right += 1 # 다음 가능성을 위해 right 이동
temp += right # 이동된 right 값을 합에 추가
print(count) # 가능한 수열의 개수 출력