Python을 이용한 1940번 : 주몽에 대해서 포스팅하겠습니다. 1940번은 정렬과 투포인터로 분류되는 문제입니다.
1. 1940번 문제설명
- 입력:
- 재료의 개수 𝑁N: 첫 번째 줄에 주어지며, 최대 15,000개까지 가능합니다.
- 갑옷을 만드는 데 필요한 수 𝑀M: 두 번째 줄에 주어지며, 갑옷을 만드는데 필요한 두 재료의 합입니다. 최대 10,000,000입니다.
- 재료들의 고유한 번호: 세 번째 줄에 공백으로 구분되어 주어집니다. 각 번호는 100,000 이하의 자연수입니다.
- 목표:
- 주어진 재료들 중 두 개를 선택하여 그 합이 정확히 M이 되는 조합의 개수를 찾는 것입니다.
- 출력:
- 첫째 줄에 M을 만들 수 있는 갑옷의 조합 수를 출력합니다.
2. 1940번 접근방법
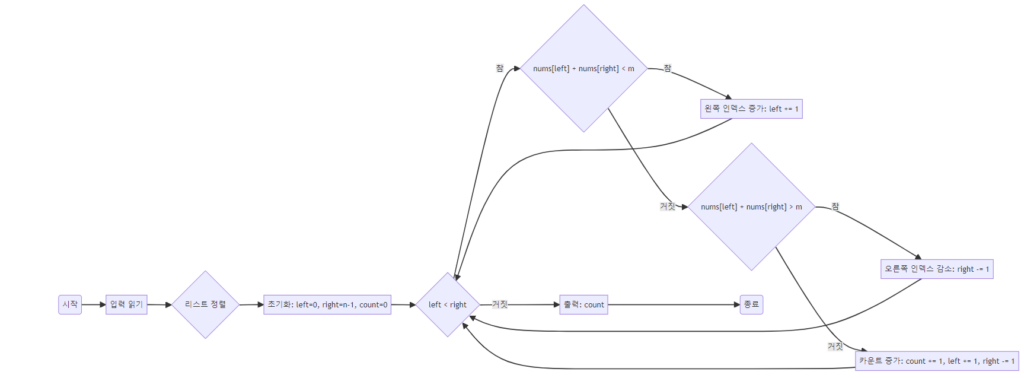
- 이 문제는 주어진 재료의 고유 번호 리스트에서 두 수를 선택하여 그 합이 주어진 수 M과 정확히 일치하는 경우의 수를 찾는 문제입니다. 이를 효율적으로 해결하기 위해 재료의 번호를 정렬한 후 두 포인터 알고리즘을 사용하여 O(NlogN)의 시간 복잡도로 문제를 해결할 수 있습니다.
3. 1940번 구현
- 두 포인터 알고리즘을 사용하여
left는 리스트의 시작을,right는 끝을 가리키며 조건에 따라 인덱스를 조정합니다. 두 수의 합이m과 동일할 때count를 증가시키고, 두 포인터를 모두 움직입니다.
3-1. 1940번 코드
Python
# https://www.acmicpc.net/problem/11048
from sys import stdin
# 미로의 크기 N과 M을 입력 받습니다.
n, m = map(int, stdin.readline().split())
# 미로의 각 칸에 놓인 사탕 수를 입력 받아 2차원 배열로 저장합니다.
nums = list(map(lambda a: list(map(int, a.split())), stdin.readlines()))
# 이중 반복문을 사용하여 미로의 모든 칸을 순회합니다.
for i in range(n):
for j in range(m):
# (1, 1) 위치는 시작 위치로, 여기서의 사탕 개수는 이미 초기 값으로 설정되어 있습니다.
if i == 0 and j == 0:
continue
# 첫 번째 행의 칸들은 왼쪽에서 오른쪽으로만 이동 가능합니다.
# 따라서 왼쪽 칸에서 오는 것만 고려합니다.
if i == 0:
nums[i][j] += nums[i][j-1]
continue
# 첫 번째 열의 칸들은 위에서 아래로만 이동 가능합니다.
# 따라서 위쪽 칸에서 오는 것만 고려합니다.
if j == 0:
nums[i][j] += nums[i-1][j]
continue
# 그 외의 경우, 준규는 (r+1, c), (r, c+1), (r+1, c+1) 세 방향으로 이동할 수 있습니다.
# 이 중에서 사탕 수가 최대가 되는 방향을 선택합니다.
# max 함수를 사용하여 세 방향 중 최대 사탕 수를 현재 칸에 더합니다.
nums[i][j] += max(nums[i-1][j], nums[i][j-1], nums[i-1][j-1])
# 결과로 (N, M) 위치의 최대 사탕 수를 출력합니다.
print(nums[-1][-1])