백준 1766 문제집

Python을 이용한 1766번 : 문제집에 대해서 포스팅하겠습니다. 1766번은 자료 구조, 그래프 이론, 우선순위 큐, 위상 정렬, 방향 비순환 그래프로 분류되는 문제입니다.

1. 1766번 문제설명

입력

1. 첫째 줄: 문제의 수 N (1 ≤ N ≤ 32,000)과 문제 간의 순서쌍의 수 M (1 ≤ M ≤ 100,000)
2. 둘째 줄부터 M개의 줄에 걸쳐 두 정수 A, B가 주어지며, 이는 A번 문제는 B번 문제보다 먼저 풀어야 한다는 의미입니다.

목표

1. 모든 문제를 풀어야 합니다.
2. ‘먼저 푸는 것이 좋은 문제’가 있는 경우, 그 문제를 먼저 풀어야 합니다.
3. 가능한 쉬운 문제부터 풀어야 합니다.

출력

1. 문제를 풀 순서를 1 이상 N 이하의 정수로 공백을 사이에 두고 출력합니다.

2. 1766번 접근방법

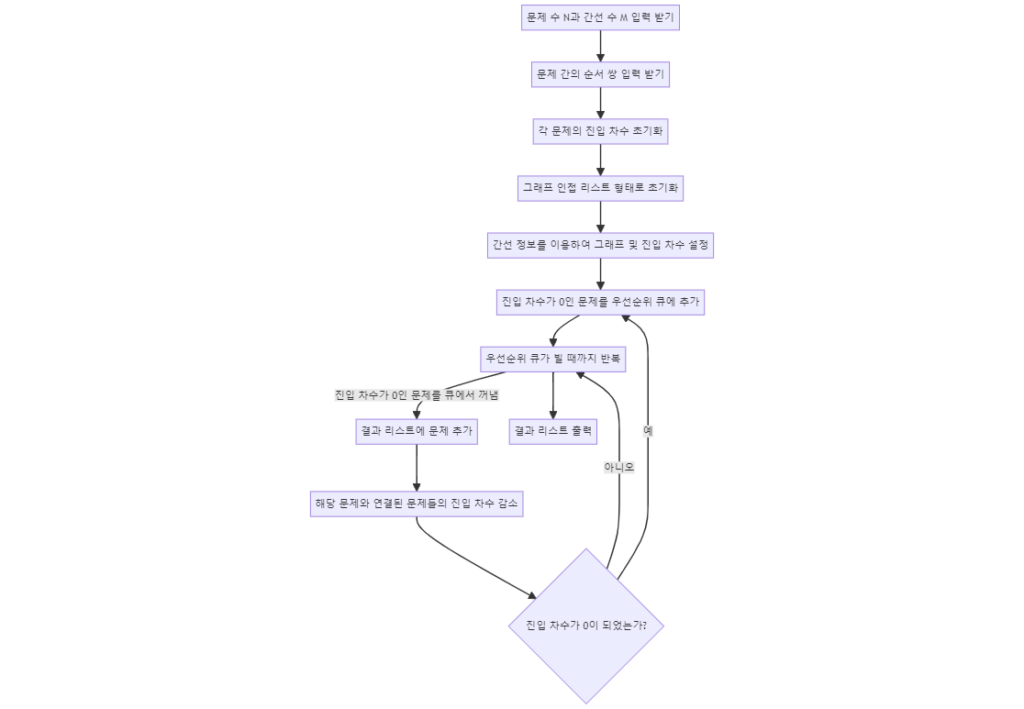
• 1. 위상 정렬(Topological Sorting)
  • 위상 정렬은 유향 그래프의 정점을 선형으로 정렬하는 알고리즘입니다. 이 정렬은 모든 간선 (u, v)에 대해 u가 v보다 먼저 오는 순서를 만족합니다. 주로 작업 스케줄링 문제나 의존성 해결 문제에 사용됩니다. 위상 정렬은 보통 큐를 사용한 Kahn’s Algorithm과 스택을 사용한 DFS 방법이 있습니다. 이 문제에서는 Kahn’s Algorithm을 사용하여 큐에 진입 차수가 0인 노드를 먼저 넣고, 이 노드와 연결된 간선을 제거하며 정렬을 진행합니다.
• 2. 힙(Heap)을 이용한 우선순위 큐
  • 힙은 이진 트리 구조를 가지며, 최소 힙과 최대 힙으로 나뉩니다. 이 문제에서는 최소 힙을 사용하여 우선순위 큐를 구현했습니다. 최소 힙에서는 루트 노드가 항상 가장 작은 값을 가지므로, 매번 가장 작은 값을 빠르게 추출할 수 있습니다. heapq 모듈을 사용하여 파이썬에서 힙을 구현하며, heappush와 heappop 함수를 통해 요소를 추가하고 제거합니다. 이 방법은 항상 쉬운 문제부터 푸는 것을 보장해줍니다.
• 3. 진입 차수(Indegree)
  • 진입 차수는 특정 노드로 들어오는 간선의 개수를 의미합니다. 위상 정렬에서 진입 차수가 0인 노드는 다른 노드에 의해 선행되어야 할 필요가 없는 노드입니다. 즉, 바로 처리할 수 있는 노드입니다. 이 문제에서는 각 문제의 진입 차수를 계산하여, 진입 차수가 0인 노드를 우선순위 큐에 넣습니다. 그런 다음 해당 노드와 연결된 간선을 제거하여 다른 노드의 진입 차수를 감소시킵니다.
• 4. 그래프 표현 방법
  • 그래프는 노드와 간선으로 구성된 자료구조입니다. 이 문제에서는 인접 리스트를 사용하여 그래프를 표현했습니다. 인접 리스트는 각 노드에 대해 그 노드와 직접 연결된 노드들을 리스트 형태로 저장합니다. 예를 들어, 문제 1이 문제 3보다 먼저 풀어야 한다면, 리스트의 1번 인덱스에 3을 추가합니다. 이 방식은 메모리 효율성이 높고, 특정 노드와 연결된 모든 노드를 찾는 데 용이합니다.

3. 1766번 구현

1. 그래프 초기화
2. 진입 차수가 0인 문제들을 우선순위 큐에 추가
3. 위상 정렬 수행

3-1. 1766번 코드

# https://www.acmicpc.net/problem/1766
from sys import stdin
import heapq

# 첫 번째 줄에서 문제의 수 N과 간선의 수 M을 입력받습니다. 이 두 값은 문제들과 문제들 간의 관계의 수를 의미합니다.
N, M = map(int, stdin.readline().split())

# 문제 간의 순서 쌍을 입력받습니다. 입력은 두 번째 줄부터 M개의 줄에 걸쳐 주어지며, 각 줄에는 두 숫자 a, b가 주어집니다.
# 이는 a번 문제가 b번 문제보다 먼저 풀어야 함을 의미합니다.
nums = list(map(lambda a: list(map(int, a.split())), stdin.readlines()))

# 각 문제의 진입 차수를 저장할 리스트를 초기화합니다. 진입 차수는 해당 문제로 들어오는 간선의 수를 의미합니다.
directed = [0 for i in range(N + 1)]

# 그래프를 인접 리스트 형태로 표현하기 위해 초기화합니다. 각 문제에서 다른 문제로 가는 관계를 저장합니다.
graph = [[] for i in range(N + 1)]
for (a, b) in nums:
    # a번 문제는 b번 문제보다 먼저 풀어야 함을 그래프에 기록합니다.
    graph[a].append(b)
    # b번 문제의 진입 차수를 증가시킵니다.
    directed[b] += 1

# 진입 차수가 0인 문제들을 우선순위 큐에 추가합니다. 진입 차수가 0인 문제는 선행되어야 하는 다른 문제가 없는 문제입니다.
queue = []
for i in range(1, N + 1):
    if directed[i] == 0:
        heapq.heappush(queue, i)

# 결과를 저장할 리스트를 초기화합니다.
result = []
# 우선순위 큐가 비어있지 않은 동안 반복합니다. 큐에서 문제를 하나씩 꺼내 결과 리스트에 추가하고, 해당 문제와 연결된 다른 문제들의 진입 차수를 감소시킵니다.
while queue:
    # 큐에서 진입 차수가 0인 문제를 꺼내어 결과 리스트에 추가합니다.
    temp = heapq.heappop(queue)
    result.append(temp)
    # 해당 문제와 연결된 문제들의 진입 차수를 감소시킵니다.
    for i in graph[temp]:
        directed[i] -= 1
        # 진입 차수가 0이 되면 큐에 추가합니다. 진입 차수가 0이 되었다는 것은 이제 이 문제를 풀어도 좋다는 의미입니다.
        if directed[i] == 0:
            heapq.heappush(queue, i)

# 결과 리스트를 공백으로 구분하여 출력합니다.
print(" ".join(map(str, result)))