백준 1449 – 수리공 항승

Python을 이용한 1449번 : 수리공 항승에 대해서 포스팅하겠습니다. 1449번은 그리디 알고리즘, 정렬 알고리즘으로 분류되는 문제입니다.

1. 1449번 문제설명

• 입력
  • 물 새는 곳의 개수(N): 파이프에서 물이 새는 위치의 총 개수를 나타냅니다. 이 값은 1,000보다 작거나 같은 자연수입니다.
  • 테이프의 길이(L): 수리공 항승이 사용할 수 있는 테이프의 길이입니다. 이 또한 1,000보다 작거나 같은 자연수입니다.
  • 물 새는 곳의 위치: 실제로 물이 새고 있는 위치들이 정수로 주어집니다. 각 위치는 1,000보다 작거나 같은 자연수로 표현됩니다.
• 목표
  • 주어진 물 새는 위치들을 모두 덮을 수 있는 테이프의 최소 개수를 찾는 것입니다.
  • 각 물 새는 위치를 덮을 때는 그 위치의 좌우로 0.5만큼의 여유를 두어야 합니다. 즉, 각 위치는 실제로 그 위치보다 0.5만큼 더 넓게 테이프로 덮어야 합니다.
  • 테이프는 자를 수 없으며, 여러 조각을 겹쳐 붙이는 것도 가능합니다.
• 출력:
  • 수리공 항승이가 모든 물 새는 위치를 덮기 위해 필요한 테이프의 최소 개수를 출력합니다.

2. 1449번 접근방법

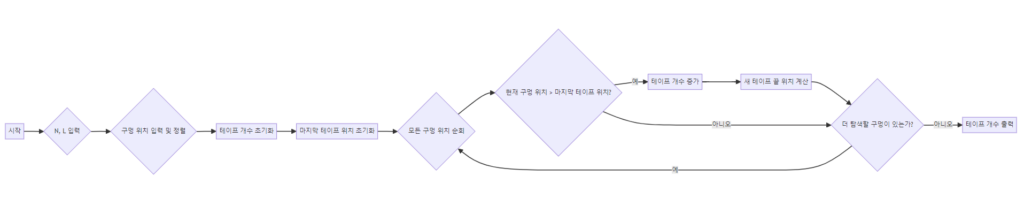
1. 입력 받기: 먼저, 물이 새는 곳의 개수 N과 테이프의 길이 L을 입력 받습니다. 그리고 물이 새는 각 위치를 나타내는 배열을 입력 받은 후 오름차순으로 정렬합니다. 정렬하는 이유는 테이프를 순차적으로 붙여나가며 모든 누수 위치를 커버하기 위함입니다.
2. 테이프 붙이기 시작하기: 배열을 순회하면서 현재 위치에서 테이프를 붙였을 때 커버할 수 있는 최대 범위를 계산합니다. 이 때, 각 물 새는 위치에 대해 좌우로 0.5만큼 여유를 두어야 하므로, 실제로 테이프를 붙이는 위치는 물 새는 위치 - 0.5가 됩니다. 그리고 이 위치부터 테이프 길이 L만큼 덮을 수 있습니다.
3. 테이프 개수 계산하기: 첫 번째 위치에서 테이프를 붙이기 시작하여, 해당 테이프로 커버할 수 있는 범위를 계산합니다. 만약 다음 물 새는 위치가 현재 테이프로 커버 가능한 범위를 벗어난다면, 새로운 테이프를 추가하고 그 위치부터 다시 커버할 수 있는 범위를 계산합니다. 이 과정을 모든 물 새는 위치를 커버할 때까지 반복합니다.
4. 출력: 필요한 테이프의 최소 개수를 출력합니다.

2-1. 예시

예를 들어, 물이 새는 위치가 [1, 2, 100, 101]이고 테이프의 길이가 2라면, 첫 번째 테이프는 위치 1에서 시작하여 위치 2.5까지 덮을 수 있습니다. 그러나 위치 100은 첫 번째 테이프로는 덮을 수 없으므로, 새로운 테이프가 필요하고, 이 두 번째 테이프는 위치 100에서 시작하여 최소 101을 덮을 수 있습니다. 따라서 필요한 테이프의 개수는 2개입니다.

3. 1449번 구현

1. 변수 설명:
   • num: 현재 순회 중인 물 새는 구멍의 위치.
   • loc: 마지막으로 사용된 테이프가 덮는 범위의 마지막 위치. 즉, 이 위치까지 현재까지 사용된 테이프로 덮을 수 있음을 의미합니다.
   • tape_count: 현재까지 사용한 테이프의 개수.
2. 테이프 사용 판단:
   • 항승이는 물 새는 파이프의 위치가 담긴 nums 배열을 가지고 작업을 시작합니다. 이 배열에는 물이 새는 각 위치가 정수 형태로 저장되어 있습니다. 항승이의 첫 번째 작업은 이 배열을 순회하며 각 위치(num)에 대해 테이프를 사용할지 결정하는 것입니다.
   • 물 새는 위치 num이 마지막으로 사용된 테이프가 덮는 범위(loc)보다 클 경우, 즉, 현재 검사하는 구멍이 이전에 붙인 테이프로 덮이지 않는 경우, 새로운 테이프를 사용해야 합니다. 이는 현재의 구멍이 이전 테이프의 덮는 범위를 벗어났음을 의미합니다.
3. 새 테이프 붙이기:
   • 새 테이프를 사용한다고 결정되면 tape_count를 1 증가시켜 사용한 테이프의 수를 갱신합니다.
   • 새로 사용하는 테이프의 덮을 수 있는 마지막 위치를 계산하여 loc을 갱신합니다. 새 테이프의 길이가 L이고, 현재 구멍의 위치가 num일 때, 이 테이프는 num부터 시작해 L-1만큼 더 덮을 수 있습니다. 예를 들어, 테이프 길이가 4이고 현재 구멍 위치가 2라면, 이 테이프는 위치 2부터 위치 5까지 (즉, 2, 3, 4, 5의 네 위치를) 덮을 수 있으므로 loc는 num + L - 1로 설정됩니다.

3-1. 1449번 코드

# https://www.acmicpc.net/problem/1449
from sys import stdin

# N: 구멍이 난 위치의 수, L: 테이프의 길이
N, L = map(int, stdin.readline().split())
# 구멍이 난 위치를 입력받아 리스트로 변환 후 정렬
nums = list(map(int, stdin.readline().split()))
nums.sort()
# 사용할 테이프의 수
tape_count = 0
# 마지막으로 테이프를 붙인 위치
loc = 0

# 구멍 위치를 순회하며 필요한 테이프 수 계산
for num in nums:
    # 현재 검사하는 구멍의 위치가 마지막으로 붙인 테이프의 끝 위치보다 클 경우, 즉 현재 구멍이 이전에 붙인 테이프로 덮이지 않는 경우
    if num > loc:
        # 새로운 테이프를 사용해야 하므로 테이프 사용 개수를 1 증가시킴
        tape_count += 1
        # 새로운 테이프를 붙이므로, 이 테이프가 덮을 수 있는 마지막 위치를 갱신함.
        # 새 테이프의 길이가 L이므로, 현재 구멍 위치(num)에서 시작해 L-1 만큼 더 덮을 수 있음.
        # 예를 들어, 테이프 길이가 4이고 현재 구멍 위치가 2라면, 이 테이프는 2, 3, 4, 5 위치를 덮을 수 있으므로
        # loc는 2 + 4 - 1 = 5가 되어, 다음 구멍 위치가 5보다 큰 경우에만 새 테이프를 붙일 필요가 있음.
        loc = num + L - 1
# 필요한 테이프 수 출력
print(tape_count)

3-2. 마무리

1449번은 그리디 알고리즘을 사용합니다. 저는 1449번을 풀면서 loc를 계산하는 부분에서 많은 착오가 있었습니다!