Python을 이용한 2805번 : 나무 자르기에 대해서 포스팅하겠습니다. 2805번은 이분 탐색, 매개 변수 탐색의 알고리즘으로 분류되는 문제입니다.
2805번 문제설명
- 입력
- 첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
- 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
- 출력
- 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
2805번 접근방법
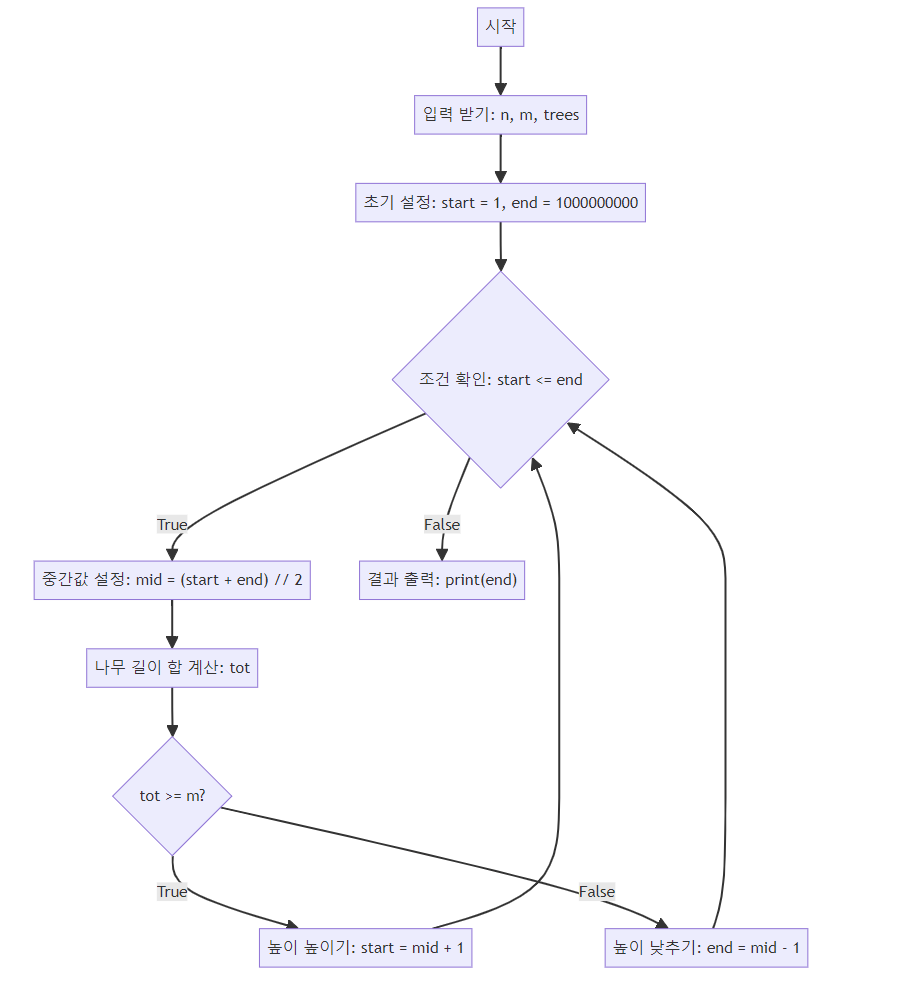
1. 2805번 알고리즘 설명
- 입력 처리: 이 코드는 표준 입력을 사용하여 데이터를 읽습니다. sys.stdin.readline()은 라인 단위로 입력을 받으며, map 함수를 사용하여 문자열을 정수로 변환합니다.
- 데이터 구조: Counter 클래스는 각 나무 높이의 등장 횟수를 계산합니다. 이는 나중에 각 높이별 나무의 총 길이를 빠르게 계산하는 데 도움을 줍니다.
- 이진 탐색: 코드는 start와 end를 조정하여 이진 탐색을 수행합니다. 이진 탐색은 로그 시간 복잡도를 가지며, 큰 데이터셋에서 높은 효율을 보입니다.
- 중간값 계산과 조건 검사: mid는 절단기의 높이를 나타내며, 이를 기준으로 나무 길이의 총합(total)을 계산합니다. total이 목표 길이(m) 이상이면 start를 조정하고, 그렇지 않으면 end를 조정합니다.
2. collections 모듈의 Counter 클래스
- 개념: Counter는 특정 데이터에서 각 요소가 몇 번 등장하는지를 카운트하는 데 사용됩니다. 이 문제에서 Counter의 역할을 구체적으로 살펴보겠습니다.
Python
trees = Counter(map(int, sys.stdin.read().split()))- 위 코드에서 Counter는 나무 높이들의 리스트를 입력 받아 각 높이별로 나무가 몇 그루인지를 계산합니다. 예를 들어, 입력된 나무 높이들이 [20, 15, 10, 20, 15]라면, Counter는 {20: 2, 15: 2, 10: 1}과 같은 결과를 반환합니다. 이는 높이가 20인 나무가 2그루, 15인 나무가 2그루, 10인 나무가 1그루 있음을 의미합니다.
- 이 정보는 이진 탐색 과정에서 중요합니다. 중간값 mid를 기준으로 나무를 잘랐을 때 얻을 수 있는 총 나무 길이를 계산할 때, 각 높이별 나무 수를 고려해야 합니다.
Python
tot = sum((h - mid) * i for h, i in trees.items() if h > mid)- 위 코드는 각 나무 높이(h)가 mid보다 클 경우, h – mid만큼의 나무 길이를 얻을 수 있으며, 이를 해당 나무 높이의 나무 수(i)만큼 곱하여 총 나무 길이(tot)를 계산합니다. 이를 통해 필요한 나무 길이(m)를 얻기 위해 설정해야 하는 절단기의 높이를 효율적으로 찾을 수 있습니다.
3. 2805번 코드
Python
import sys
from collections import Counter
# 입력 받기:
# n은 나무의 수, m은 필요한 나무 길이의 합
# sys.stdin.readline()을 통해 한 줄을 읽어 정수형으로 변환 후 n, m에 할당
n, m = map(int, sys.stdin.readline().split())
# 다음 줄을 읽어 나무의 높이를 리스트로 변환 후 Counter 객체로 변환하여 각 높이별 나무 수를 계산
trees = Counter(map(int, sys.stdin.read().split()))
# 초기 설정:
# 이진 탐색을 위한 시작점 start와 끝점 end 설정
start = 1 # 가능한 최소 높이
end = 1000000000 # 가능한 최대 높이
# 이진 탐색 시작:
while start <= end:
mid = (start + end) // 2 # 중간값 설정, 절단기 높이를 의미
# 나무를 중간값 높이로 잘랐을 때 얻을 수 있는 나무 길이의 총합 계산
# 나무 높이가 mid보다 클 경우에만 (나무 높이 - mid)를 계산하여 합산
total = sum((height - mid) * count for height, count in trees.items() if height > mid)
# 총합이 목표 길이 m 이상인 경우
# 더 높은 높이에서 잘라도 충분할 수 있으므로, 시작점 start를 중간값보다 1 높게 설정
if total >= m:
start = mid + 1
# 총합이 목표 길이 m 미만인 경우
# 더 낮은 높이에서 잘라야 하므로, 끝점 end를 중간값보다 1 낮게 설정
elif total < m:
end = mid - 1
# 최적의 절단기 높이 출력
# while 루프를 벗어난 후의 end 값은 필요한 길이를 만족하는 최대 절단기 높이를 의미
print(end)