Python을 이용한 7576번 : 토마토에 대해서 포스팅하겠습니다. 7576번은 그래프 이론, 그래프 탐색, 너비 우선 탐색으로 분류되는 문제입니다.
1. 7576번 문제설명
- 입력
- 상자의 크기: 두 정수 M,N 으로 표현되며, M은 상자의 가로 칸 수, N은 상자의 세로 칸 수를 나타냅니다. (2≤M,N≤1,000)
- 토마토의 상태: 상자 내의 토마토 상태가 N개의 줄에 걸쳐 주어지며, 각 줄에는 M개의 정수로 표현됩니다. 이 정수들은 다음을 의미합니다:
- 1: 익은 토마토
- 0: 익지 않은 토마토
- -1: 토마토가 들어있지 않은 칸
- 목표
- 모든 토마토가 익는 최소 일수 계산: 상자 안에 있는 모든 토마토가 익을 때까지 걸리는 최소 일수를 계산합니다. 익은 토마토는 인접한 칸(상하좌우)에 있는 익지 않은 토마토를 다음 날에 익게 만듭니다.
- 출력
- 모든 토마토가 익는 최소 일수: 만약 모든 토마토가 처음부터 익어있다면 0을 출력합니다.
- 토마토가 모두 익지 못하는 상황: 상자 안의 토마토 중 하나라도 익지 못하는 경우 -1을 출력합니다.
2. 7576번 접근방법
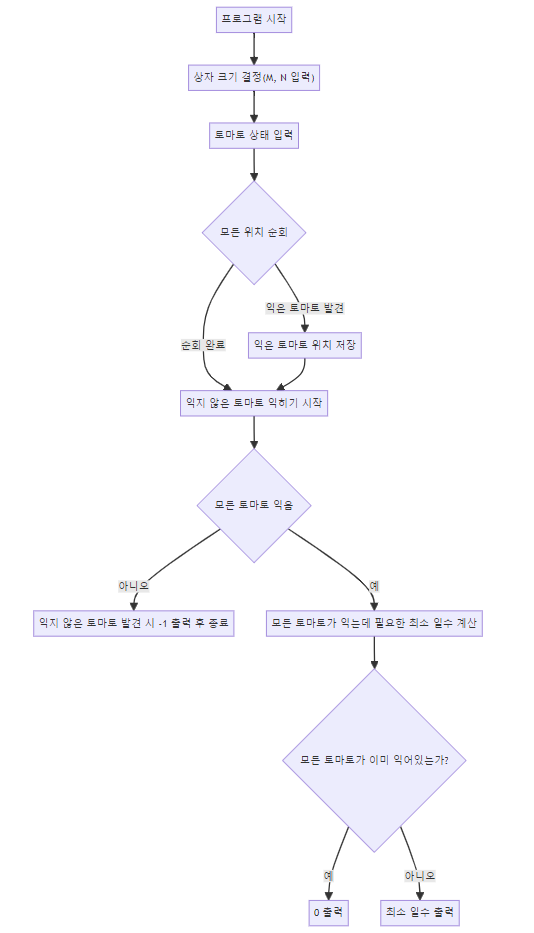
- 입력 받기: 먼저, 창고의 가로(
M), 세로(N) 크기와 함께 각 칸에 대한 토마토의 상태(익은 토마토1, 익지 않은 토마토0, 토마토 없음-1)를 입력 받습니다. - 익은 토마토 위치 파악: 익은 토마토의 위치를 찾아 큐(queue)에 저장합니다. 이 큐는 BFS를 수행하는 데 사용됩니다.
- BFS 실행: 큐에서 하나씩 위치를 꺼내어 그 위치의 토마토가 인접한 익지 않은 토마토를 익게 합니다. 이때, 상하좌우 네 방향만을 고려합니다. 익게 된 토마토의 위치도 다시 큐에 넣어주어, 모든 토마토가 익을 때까지 이 과정을 반복합니다.
- 결과 계산 및 출력: 모든 토마토가 익는 데 필요한 최소 일수를 계산하여 출력합니다. 만약 모든 토마토가 처음부터 익어있는 상태라면
0, 토마토가 모두 익지 못하는 상황이면-1을 출력합니다.
3. 7576번 구현
- 입력 받기: 먼저, 창고의 가로(
M), 세로(N) 크기와 함께 각 칸에 대한 토마토의 상태(익은 토마토1, 익지 않은 토마토0, 토마토 없음-1)를 입력 받습니다. - 익은 토마토 위치 파악: 익은 토마토의 위치를 찾아 큐(queue)에 저장합니다. 이 큐는 BFS를 수행하는 데 사용됩니다.
- BFS 실행: 큐에서 하나씩 위치를 꺼내어 그 위치의 토마토가 인접한 익지 않은 토마토를 익게 합니다. 이때, 상하좌우 네 방향만을 고려합니다. 익게 된 토마토의 위치도 다시 큐에 넣어주어, 모든 토마토가 익을 때까지 이 과정을 반복합니다.
- 결과 계산 및 출력: 모든 토마토가 익는 데 필요한 최소 일수를 계산하여 출력합니다. 만약 모든 토마토가 처음부터 익어있는 상태라면
0, 토마토가 모두 익지 못하는 상황이면-1을 출력합니다.
3-1. 7576번 코드
Python
# https://www.acmicpc.net/problem/7576
from sys import stdin
from collections import deque
# 입력값을 받아와서 상자의 크기를 결정합니다. M은 가로 칸의 수, N은 세로 칸의 수입니다.
M,N = map(int,stdin.readline().split())
# 상자에 담긴 토마토의 상태를 2차원 리스트로 저장합니다. 익은 토마토는 1, 익지 않은 토마토는 0, 토마토가 없는 칸은 -1로 표시됩니다.
graph = list(map(lambda a : list(map(int,a.split())), stdin.read().splitlines()))
# 익은 토마토를 찾아서 주변의 익지 않은 토마토를 익게 하는 함수입니다.
def grow_tomato(queue) :
global graph # 전역 변수인 graph를 함수 내에서 수정하기 위해 선언합니다.
while queue : # queue에 요소가 있을 동안 반복합니다.
i,j = queue.popleft() # 현재 위치를 queue에서 꺼냅니다.
for px, py in [(0,1),(1,0),(-1,0),(0,-1)] : # 현재 위치에서 상하좌우를 탐색합니다.
nx,ny = i+px, j+py # 다음 위치를 계산합니다.
# 다음 위치가 상자 내부에 있고, 익지 않은 토마토가 있는 경우
if 0<=nx<N and 0<=ny<M and graph[nx][ny] == 0 :
graph[nx][ny] = graph[i][j] + 1 # 다음 위치의 토마토를 익게 하고, 날짜를 기록합니다.
queue.append((nx,ny)) # 익은 토마토의 위치를 queue에 추가합니다.
queue = deque()
# 모든 위치를 순회하면서 익은 토마토의 위치를 찾아 queue에 추가합니다.
for i in range(N) :
for j in range(M) :
if graph[i][j] == 1 :
queue.append((i,j))
grow_tomato(queue) # 익은 토마토로부터 시작하여 모든 토마토를 익게 하는 함수를 호출합니다.
# 모든 토마토가 익는 데 필요한 최소 일수를 계산합니다.
answer = 0
for i in range(N):
for j in range(M):
if graph[i][j] == 0: # 익지 않은 토마토가 있는 경우
print(-1)
exit(0)
answer = max(answer, graph[i][j]) # 모든 토마토가 익는데 걸린 최대 날짜를 찾습니다.
# 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력합니다.
if answer == 1:
print(0)
else:
print(answer - 1) # 최소 일수는 최대값에서 1을 빼서 계산합니다.